初中数学规律型：图形的变化类选择题

一根绳子弯曲成如图1所示的形状．当用剪刀像图2那样沿虚线a把绳子剪断时，绳子被剪为5段；当用剪刀像图3那样沿虚线b（b∥a）把绳子再剪一次时，绳子就被剪为9段．若用剪刀在虚线a，b之间把绳子再剪（n2）次（剪刀的方向与a平行），这样一共剪n次时绳子的段数是（   ）．

A．4n+1

B．4n+2

C．4n+3

D．4n+5

如图，在平面直角坐标系 $\mathit{xOy}$中，直线 $y=-\frac{1}{3}x+\frac{13}{3}$分别与 $x$轴、 $y$轴交于点 $P$、 $Q$，在 $\text{Rt}\Delta \text{OPQ}$中从左向右依次作正方形 $A_1{B}_1{C}_1{C}_2$、 $A_2{B}_2{C}_2{C}_3$、 $A_3{B}_3{C}_3{C}_4\dots A_n{B}_n{C}_n{C}_{n+1}$，点 $A_1$、 $A_2$、 $A_3\dots A_n$在 $x$轴上，点 $B_1$在 $y$轴上，点 $C_1$、 $C_2$、 $C_3\dots C_{n+1}$在直线 $\mathit{PQ}$上；再将每个正方形分割成四个全等的直角三角形和一个小正方形，其中每个小正方形的边都与坐标轴平行，从左至右的小正方形（阴影部分）的面积分别记为 $S_1$、 $S_2$、 $S_3\dots S_n$，则 $S_n$可表示为 $($　　 $)$

A．． $\frac{3^{2n-2}}{4^{2n-3}}$B．． $\frac{3^{n-1}}{4^{n-2}}$

C．． $\frac{3^n}{4^{n-1}}$D．． $\frac{3^{2n}}{4^{2n-1}}$

下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，……，依此规律，第五个图形中三角形的个数是（  ）

A．22

B．24

C．26

D．28

如图，四边形 $\mathit{OA}{A}_1{B}_1$ 是边长为1的正方形，以对角线 $O{A}_1$ 为边作第二个正方形 $O{A}_1{A}_2{B}_2$ ，连接 $A{A}_2$ ，得到△ $A{A}_1{A}_2$ ；再以对角线 $O{A}_2$ 为边作第三个正方形 $O{A}_2{A}_3{B}_3$ ，连接 $A_1{A}_3$ ，得到△ $A_1{A}_2{A}_3$ ，再以对角线 $O{A}_3$ 为边作第四个正方形 $O{A}_2{A}_4{B}_4$ ，连接 $A_2{A}_4$ ，得到△ $A_2{A}_3{A}_4$ ， $\dots$ ，设△ $A{A}_1{A}_2$ ，△ $A_1{A}_2{A}_3$ ，△ $A_2{A}_3{A}_4$ ， $\dots$ ，的面积分别为 $S_1$ ， $S_2$ ， $S_3$ ， $\dots$ ，如此下去，则 $S_{2020}$ 的值为 $($ 　　 $)$

A．

$\frac{1}{2^{2020}}$

B．

$2^{2018}$

C．

$2^{2018}+\frac{1}{2}$

D．

1010

小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体， $\dots$按照此规律，从第 $\left(100\right)$个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是 $($　　 $)$

A． $\frac{1}{100}$B． $\frac{1}{20}$C． $\frac{1}{101}$D． $\frac{2}{101}$

如图，每一幅图中均含有若干个正方形，第①幅图中含有1个正方形；第②幅图中含有5个正方形；第③幅图中含有14个正方形．按这样的规律下去，则第⑥幅图中含有正方形的个数为（   ）

A．55

B．78

C．91

D．140

下列图中所有小正方形都是全等的．图（1）是一张由4个小正方形组成的" $L$ "形纸片，图（2）是一张由6个小正方形组成的 $3\times 2$ 方格纸片．

把" $L$ "形纸片放置在图（2）中，使它恰好盖住其中的4个小正方形，共有如图（3）中的4种不同放置方法．图（4）是一张由36个小正方形组成的 $6\times 6$ 方格纸片，将" $L$ "形纸片放置在图（4）中，使它恰好盖住其中的4个小正方形，共有 $n$ 种不同放置方法，则 $n$ 的值是 $($ 　　 $)$

A．

160

B．

128

C．

80

D．

48

如图，将矩形 $\mathit{ABCD}$绕其右下角的顶点按顺时针方向旋转 $90°$至图①位置，继续绕右下角的顶点按顺时针方向旋转 $90°$至图②位置，以此类推，这样连续旋转2017次．若 $\mathit{AB}=4$， $\mathit{AD}=3$，则顶点 $A$在整个旋转过程中所经过的路径总长为 $($　　 $)$

A． $2017\pi$B． $2034\pi$C． $3024\pi$D． $3026\pi$

如图，用火柴棍拼成一排由三角形组成的图形，如果图形中含有16个三角形，则需要（ ）根火柴棍．

A．30根

B．31根

C．32根

D．33根

人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，如图中的每一个小正方形表示一块地砖．如果按图①②③ $\dots$的次序铺设地砖，把第 $n$个图形用图 $?$表示，那么第50个图形中的白色小正方形地砖的块数是 $($　　 $)$

A．150B．200C．355D．505

我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1，3，6，10…）和“正方形数”（如1，4，9，16…），在小于200的数中，设最大的“三角形数”为 $m$，最大的“正方形数”为 $n$，则 $m+n$的值为 $($　　 $)$

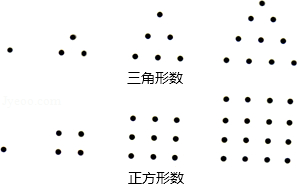
A．33B．301C．386D．571

如图，小聪用一张面积为1的正方形纸片，按如下方式操作：

①将正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，把四个等腰直角三角形扔掉；

②在余下纸片上依次重复以上操作，当完成第2019次操作时，余下纸片的面积为（　　）

A．

2 ^2019

B．

$\frac{1}{2^{2018}}$

C．

$\frac{1}{2^{2019}}$

D．

$\frac{1}{2^{2020}}$

一质点P从距原点1个单位的M点处向原点方向跳动，第一次跳动到OM的中点M₁处，第二次从M₁跳到OM₁的中点M₂处，第三次从点M₂跳到OM₂的中点M₃处，如此不断跳动下去，则第n次跳动后，该质点到原点O的距离为（   ）

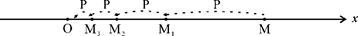
A．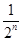

B．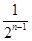

C．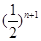

D．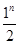

数学兴趣小组同学从"中国结"的图案（图 $1)$ 中发现，用相同的菱形纵向排列放置，可得到更多的菱形．如图2，用2个相同的菱形放置，得到3个菱形．下面说法正确的是 $($ 　　 $)$

A．	用3个相同的菱形放置，最多能得到6个菱形
B．	用4个相同的菱形放置，最多能得到16个菱形
C．	用5个相同的菱形放置，最多能得到27个菱形
D．	用6个相同的菱形放置，最多能得到41个菱形

由12个有公共顶点 $O$ 的直角三角形拼成的图形如图所示， $\angle \mathit{AOB}=\angle \mathit{BOC}=\dots =\angle \mathit{LOM}=30°$ ．若 $\mathit{OA}=16$ ，则 $\mathit{OG}$ 的长为 $($ 　　 $)$

A．

$\frac{27}{4}$

B．

$\frac{1}{4}$

C．

$\frac{9\sqrt{3}}{2}$

D．

$\frac{27\sqrt{3}}{8}$