初中数学整式的加减试题

（每题4分，本题满分12分）（1）先化简，再求值
5（3a²b－ab²）－4（－ab²＋3a²b），其中a＝－1，b＝2．
（2）某同学在计算多项式M加上x²－3x＋7时，因误认为是加上x²＋3x＋7，结果得到答案是15x²＋2x－4．试问：（1）M是怎样的整式？（2）这个问题的正确结果应是多少？
（3）“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．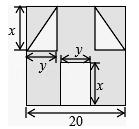

①用含有x、y的代数式表示右图中“囧”的面积；
②当x=4，y=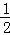时，求此时“囧”的面积

甲从一个鱼摊买三条鱼，平均每条元，又从另一个鱼摊买了两条鱼，平均每条元，后来他又以每条元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是      （ ）

A．

B．

C．

D．与和大小无关

（本题5分）已知,
（1）求的值；（结果用x、y表示）
（2）当与互为相反数时，求（1）中代数式的值．

（本题8分）如图，在数轴上A点表示数a，B点表示数b,AB表示A点和B点之间的距离，且a、b满足．

（1）求A、B两点之间的距离；
（2）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动．设运动的时间为t（秒），
①分别表示甲、乙两小球到原点的距离（用t表示）；
②求甲、乙两小球到原点的距离相等时经历的时间．

化简求值（每题5分，共15分）
（1）先化简再求值：，其中
（2）已知有理数a,b,c在数轴上的位置如图,试化简代数式：|b|－|c+b|+|c＋a|+|b－a|．

（3）已知关于x、y的多项式合并后不含有二次项，求的值．

为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段以达到节水的目的. 该市自来水收费价格见价目表.

（1）填空：若该户居民2月份用水4m³,则应收水费          元；
（2）若该户居民3月份用水am³（其中6<a<10），则应收水费多少元？（用a的整式表示并化简）
（3）若该户居民4,5月份共用水15m³（5月份用水量超过了4月份），设4月份用水xm³，求该户居民4,5月份共交水费多少元？（用x的整式表示并化简）

某自行车厂计划每天平均生产n辆自行车，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：

星期	一	二	三	四	五
实际生产量	+5	-2	-4	+13	-3

 
（1）用含n的代数式表示本周前三天生产自行车的总数；
（2）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，当n=100时，那么该厂工人这一周的工资总额是多少元？
（3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，则这一周工人的工资与按日计件的工资哪一个更多？请说明理由．

“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．

（1）用含有x、y的代数式表示右图中“囧”的面积；
（2）当y=,x=4时，求此时“囧”的面积.

化简或化简求值（每小题6分，共12分）
（1）|a-2|+（b+3）²=0，求3a²b-[2ab²-2（ab-1.5a²b）+ab]+3ab²的值；
（2）已知有理数a、b、c在数轴上的对应点如图所示，化简：|b-a|+|a+c|-2|c-b|．

符号“”称为二阶行列式，规定它的运算法则为：=ad-bc，例如：的计算方法为=3×4-2×5=12-10=2，请根据阅读材料化简二阶行列式   ．

某工厂第一车间有人，第二车间比第一车间人数的少30人，如果从第二车间调出10人到第一车间，那么：
（1）两个车间共有多少人？
（2）调动后，第一车间的人数比第二车间多多少人？

有这样一道题：“计算的值，其中.甲同学把“错抄成但他计算的结果也是正确的，试说明理由，并求出这个结果.

多项式与多项式的和是²，多项式与多项式的和是²，那么多项式减去多项式的差是（　　）

A．^2

B．^2

C．^2

D．^2

已知：A3B＝，B＝．
（1）求A；（用含、的代数式表示）
（2）若＝0，求A的值．

已知多项式M、N，计算M-N．某同学做此题时误将看成了，求得其结果为，若，请你帮助他求得正确答案．