仔细观察下列三组数
第一组:1、4、9、16、25……
第二组:0、3、8、15、24……
第三组:0、6、16、30、48……
解答下列问题:
(1)每一组的第6个数分别是_______、_______、_______
(2)分别写出第二组和第三组的第n个数_______、_______
(3)取每组数的第10个数,计算它们的和
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+2+22+23+…+22014的值是
阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为 ,依次类推,排在第
,依次类推,排在第 位的数称为第
位的数称为第 项,记为
项,记为 .
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 表示(
表示( ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中 ,公比为
,公比为 .
.
则:(1)等比数列3,6,12,…的公比 为 ,第4项是 .
为 ,第4项是 .
(2)如果一个数列 ,
, ,
, ,
, ,…是等比数列,且公比为
,…是等比数列,且公比为 ,那么根据定义可得到:
,那么根据定义可得到: ,
, ,
, ,……
,……  .
.
所以: ,
, ,
, ,
,
由此可得: (用
(用 和
和 的代数式表示)
的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
已知:如图,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为-30,B点对应的数为100.
(1)A、B间的距离是 ;
(2)若点C也是数轴上的点,C到B的距离是C到原点O的距离的3倍,求C对应的数;
(3)若当电子P从B点出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位长度/秒的速度向左运动,设两只电子蚂蚁在数轴上的D点相遇,那么D点对应的数是多少?
(4)若电子蚂蚁P从B点出发,以8个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从A点出,以4个单位长度/秒向右运动.设数轴上的点N到原点O的距离等于P点到O的距离的一半,有两个结论①ON+AQ的值不变;②ON-AQ的值不变.请判断那个结论正确,并求出结论的值.
某班参加校运动会的19名运动员的运动服号码恰是1~19号,这些运动员随意地站成一个圆圈,则一定有顺次相邻的某3名运动员,他们运动服号码数之和不小于32,请你说明理由.
一条公路上,有一个骑车人和一个步行人,骑车人速度是步行人速度的3倍,每隔6分钟有一辆公共汽车超过步行人,每隔10分钟有一辆公共汽车超过骑车人,如果公共汽车始发站发车的时间间隔保持不变,那么间隔几分钟发一辆公共汽车?
有一组等式:


 请观察它们的构成规律,用你发现的规律解答下面的问题:
请观察它们的构成规律,用你发现的规律解答下面的问题:
(1)写出第8个等式为 ;
(2)试用含正整数 的等式表示你所发现的规律;
的等式表示你所发现的规律;
(3)说明你在(2)中所写等式成立的理由.
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行。”国王以为要不了多少粮食,就随口答应了,结果国王输了.
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少米?(用幂表示)
(2)请探究第(1)中的数的末位数字是多少?(简要写出探究过程.)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
用分数表示无限循环小数: .
.
解:设 ①.等式两边同时乘以10,得
①.等式两边同时乘以10,得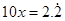 ②.
②.
将②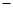 ①得:
①得: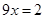 ,则
,则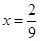 ,∴
,∴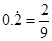 .
.
请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示).
试题篮
()