初中数学因式分解解答题

已知 $x-y=2$， $\frac{1}{x}-\frac{1}{y}=1$，求 $x^{2}y-x{y}^2$的值．

先因式分解，再计算求值： $2x^3-8x$，其中 $x=3$．

我们知道，任意一个正整数 $n$都可以进行这样的分解： $n=p\times q(p$， $q$是正整数，且 $p⩽q)$，在 $n$的所有这种分解中，如果 $p$， $q$两因数之差的绝对值最小，我们就称 $p\times q$是 $n$的最佳分解．并规定： $F\left(n\right)=\frac{p}{q}$．

例如12可以分解成 $1\times 12$， $2\times 6$或 $3\times 4$，因为 $12-1>6-2>4-3$，所以 $3\times 4$是12的最佳分解，所以 $F\left(12\right)=\frac{3}{4}$．

（1）如果一个正整数 $m$是另外一个正整数 $n$的平方，我们称正整数 $m$是完全平方数．

求证：对任意一个完全平方数 $m$，总有 $F\left(m\right)=1$；

（2）如果一个两位正整数 $t$， $t=10x+y(1⩽x⩽y⩽9$， $x$， $y$为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数 $t$为“吉祥数”，求所有“吉祥数”；

（3）在（2）所得“吉祥数”中，求 $F\left(t\right)$的最大值．

由多项式乘法： $(x+a)(x+b)=x^2+(a+b)x+\mathit{ab}$，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式： $x^2+(a+b)x+\mathit{ab}=(x+a)(x+b)$．

示例：分解因式： $x^2+5x+6=x^2+(2+3)x+2\times 3=(x+2)(x+3)$．

（1）尝试：分解因式： $x^2+6x+8=(x+$　　 $\left)\right(x+$　　 $)$；

（2）应用：请用上述方法解方程： $x^2-3x-4=0$．

已知 a+ b＝3， ab＝2，求代数式 a ³ b+2 a ² b ²+ ab ³的值．

因式分解： $a^2+\mathit{ab}-a=$ 　　．

发现 任意五个连续整数的平方和是5的倍数．

验证 （1）的结果是5的几倍？

          （2）设五个连续整数的中间一个为，写出它们的平方和，并说明是5的倍数．

延伸   任意三个连续整数的平方和被3除的余数是几呢？请写出理由．

仔细阅读下面例题，解答问题：
例题：已知二次三项式x²﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．
解：设另一个因式为（x+n），得
x²﹣4x+m=（x+3）（x+n）
则x²﹣4x+m=x²+（n+3）x+3n
∴．
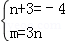解得：n=﹣7，m=﹣21
∴另一个因式为（x﹣7），m的值为﹣21
问题：仿照以上方法解答下面问题：
已知二次三项式2x²+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．

当x=21，y=101时，求xy+1﹣x﹣y的值．

运用因式分解计算：5.76²﹣4.24²．

因式分解：a²+a+．

有足够多的长方形和正方形卡片，如下图：

（1）如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．

这个长方形的代数意义是                         ．
（2）小明想用类似方法解释多项式乘法（a+3b）（2a+b）=2a²+7ab+3b²，那么需用2号卡片     张，3号卡片        张．

已知a，b，c分别是△ABC三边的长，且a²+2b²+c²-2b（a+c）=0，请判断△ABC的形状，并说明理由．

（1）计算：（2x²y）（-xy²z）³（3x²）
（2）因式分解：-8ax²+16axy-8ay²
（3）因式分解：（x²-3）²-4x²．

分解因式：（1）；（2）．