初中数学一元一次方程的应用解答题

某机电厂有甲乙两个发电机生产车间，甲车间每天产量为型发电机和型发电机共45台，其中型发电机数量比型发电机数量多5台．

（1）问甲车间每天生产、两种型号发电机各多少台？

（2）乙车间每天产量为50台，其中型发电机20台，型发电机30台，现有一订单需型发电机720台和型发电机台，但由于受原材料供应限制，两车间不能同时生产，厂里决定由甲乙两车间先后用30天完成订单任务，求甲车间至少需安排生产多少天？由于甲车间还有其他生产任务，最多只能安排27天参加此订单生产，求出所有的可能值．

某单位计划购买甲、乙两种品牌的消毒剂，乙种品牌消毒剂每瓶的价格比甲种品牌消毒剂每瓶价格的3倍少50元，已知用300元购买甲种品牌消毒剂的数量与用400元购买乙种品牌消毒剂的数量相同．

（1）求甲、乙两种品牌消毒剂每瓶的价格各是多少元？

（2）若该单位从超市一次性购买甲、乙两种品牌的消毒剂共40瓶，且总费用为1400元，求购买了多少瓶乙种品牌消毒剂？

某文明小区有50平方米和80平方米两种户型的住宅，50平方米住宅套数是80平方米住宅套数的2倍．物管公司月底按每平方米2元收取当月物管费，该小区全部住宅都人住且每户均按时全额缴纳物管费．

（1）该小区每月可收取物管费90000元，问该小区共有多少套80平方米的住宅？

（2）为建设“资源节约型社会”，该小区物管公司5月初推出活动一：“垃圾分类送礼物”，50平方米和80平方米的住户分别有和参加了此次活动．为提高大家的积极性，6月份准备把活动一升级为活动二：“垃圾分类抵扣物管费”，同时终止活动一．经调査与测算，参加活动一的住户会全部参加活动二，参加活动二的住户会大幅增加，这样，6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加，每户物管费将会减少；6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加，每户物管费将会减少．这样，参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少，求的值．

列方程解应用题

《九章算术》中有“盈不足术”的问题，原文如下：“今有共買羊，人出五，不足四十五；人出七，不足三．问人数、羊價各幾何？”题意是：若干人共同出资买羊，每人出5元，则差45元；每人出7元，则差3元．求人数和羊价各是多少？

经过一年多的精准帮扶，小明家的网络商店（简称网店）将红枣、小米等优质土特产迅速销往全国．小明家网店中红枣和小米这两种商品的相关信息如下表：

商品	红枣	小米
规格	袋	袋
成本（元袋）	40	38
售价（元袋）	60	54

根据上表提供的信息，解答下列问题：

（1）已知今年前五个月，小明家网店销售上表中规格的红枣和小米共，获得利润4.2万元，求这前五个月小明家网店销售这种规格的红枣多少袋；

（2）根据之前的销售情况，估计今年6月到10月这后五个月，小明家网店还能销售上表中规格的红枣和小米共，其中，这种规格的红枣的销售量不低于．假设这后五个月，销售这种规格的红枣为，销售这种规格的红枣和小米获得的总利润为（元，求出与之间的函数关系式，并求这后五个月，小明家网店销售这种规格的红枣和小米至少获得总利润多少元．

接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂．为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂．

（1）求该厂当前参加生产的工人有多少人？

（2）生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时．若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？

某校为改善办学条件，计划购进、两种规格的书架，经市场调查发现有线下和线上两种购买方式，具体情况如下表：

规格	线下		线上
	单价（元个）	运费（元个）		单价（元个）	运费（元个）
	240	0		210	20
	300	0		250	30

（1）如果在线下购买、两种书架20个，共花费5520元，求、两种书架各购买了多少个

（2）如果在线上购买、两种书架20个，共花费元，设其中种书架购买个，求关于的函数关系式．

（3）在（2）的条件下，若购买种书架的数量不少于种书架的2倍，请求出花费最少的购买方案，并计算按照这种购买方案线上比线下节约多少钱．

我市某校组织爱心捐书活动，准备将一批捐赠的书打包寄往贫困地区，其中每包书的数目相等．第一次他们领来这批书的 $\frac{2}{3}$，结果打了16个包还多40本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了9个包，那么这批书共有多少本？

学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．

（1）求每套课桌椅的成本；

（2）求商店获得的利润．

某超市有线上和线下两种销售方式．与2019年4月份相比，该超市2020年4月份销售总额增长 $10\%$，其中线上销售额增长 $43\%$，线下销售额增长 $4\%$．

（1）设2019年4月份的销售总额为 $a$元，线上销售额为 $x$元，请用含 $a$， $x$的代数式表示2020年4月份的线下销售额（直接在表格中填写结果）；

时间	销售总额（元 $)$	线上销售额（元 $)$	线下销售额（元 $)$
2019年4月份	$a$	$x$	$a-x$
2020年4月份	$1.1a$	$1.43x$	$1.04(a-x)$

（2）求2020年4月份线上销售额与当月销售总额的比值．

为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路．其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工．甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进26米．已知甲工程队每天比乙工程队多掘进2米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？

如图，在数轴上点A表示的数为a，点B表示的数为b，且a，b满足|a+2|+（3a+b）²=0，O为原点．

（1）则a=      ，b=      ；
（2）若动点P从点A出发，以每秒1个单位长度的速度沿数轴向右匀速运动，
①当PO=2PB时，求点P的运动时间t；
②当点P运动到线段OB上时，分别取AP和OB的中点E、F，则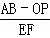的值为      ．
（3）有一动点Q从原点O出发第一次向左运动1个单位长度，然后在新的位置第二次运动，向右运动2个单位长度，在此位置第三次运动，向左运动3个单位长度…按照如此规律不断地左右运动，当运动到2015次时，求点Q所对应的有理数．

用边长为12cm的正方形硬纸板做三棱柱盒子，每个盒子的侧面为长方形，底面为等边三角形．
（1）每个盒子需      个长方形，      个等边三角形；
（2）硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）A方法：剪6个侧面；B方法：剪4侧面5个底面．

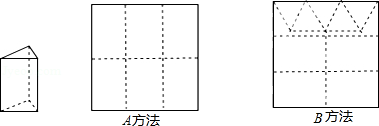
现有19张硬纸板，裁剪时x张用A方法，其余用B方法．
①用x的代数式分别表示裁剪出的侧面和底面的个数；
②若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

某工厂有甲、乙两个车间，甲车间生产 $A$ 产品，乙车间生产 $B$ 产品，去年两个车间生产产品的数量相同且全部售出．已知 $A$ 产品的销售单价比 $B$ 产品的销售单价高100元，1件 $A$ 产品与1件 $B$ 产品售价和为500元．

（1） $A$ 、 $B$ 两种产品的销售单价分别是多少元？

（2）随着 $5G$ 时代的到来，工业互联网进入了快速发展时期．今年，该工厂计划依托工业互联网将乙车间改造为专供用户定制 $B$ 产品的生产车间．预计 $A$ 产品在售价不变的情况下产量将在去年的基础上增加 $a\%$ ； $B$ 产品产量将在去年的基础上减少 $a\%$ ，但 $B$ 产品的销售单价将提高 $3a\%$ ．则今年 $A$ 、 $B$ 两种产品全部售出后总销售额将在去年的基础上增加 $\frac{29}{25}a\%$ ．求 $a$ 的值．

为改善城市人居环境，《成都市生活垃圾管理条例》（以下简称《条例》 $)$于2021年3月1日起正式施行．某区域原来每天需要处理生活垃圾920吨，刚好被12个 $A$型和10个 $B$型预处置点位进行初筛、压缩等处理．已知一个 $A$型点位比一个 $B$型点位每天多处理7吨生活垃圾．

（1）求每个 $B$型点位每天处理生活垃圾的吨数；

（2）由于《条例》的施行，垃圾分类要求提高，在每个点位每天将少处理8吨生活垃圾，同时由于市民环保意识增强，该区域每天需要处理的生活垃圾比原来少10吨．若该区域计划增设 $A$型、 $B$型点位共5个，试问至少需要增设几个 $A$型点位才能当日处理完所有生活垃圾？