如图,平面直角坐标系中,已知点 的坐标为 .
(1)请用直尺(不带刻度)和圆规作一条直线 ,它与 轴和 轴的正半轴分别交于点 和点 ,且使 , 与 的面积相等.(作图不必写作法,但要保留作图痕迹.
(2)问:(1)中这样的直线 是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线 ,并写出与之对应的函数表达式.
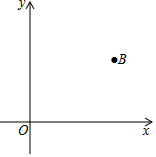
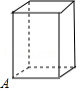
实验室里有一个水平放置的长方体容器,从内部量得它的高是 ,底面的长是 ,宽是 ,容器内的水深为 .现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点 的三条棱的长分别 , , ,当铁块的顶部高出水面 时, , 满足的关系式是 .
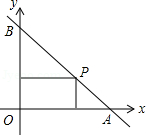
如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是
A. B. C. D.
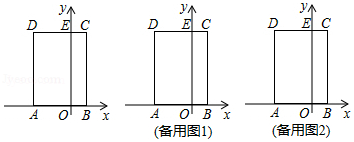
如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 运动的过程中,是否存在点 ,使 是以 为腰的等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
已知一个围棋盒子中装有7颗围棋子,其中3颗白棋子,4颗黑棋子,若往盒子中再放入 颗白棋子和 颗黑棋子,从盒子中随机取出一颗白棋子的概率为 ,则 与 之间的关系式是 .
某公司研发了一款成本为60元的保温饭盒,投放市场进行试销售,按物价部门规定,其销售单价不低于成本,但销售利润不高于 ,市场调研发现,保温饭盒每天的销售数量 (个 与销售单价 (元 满足一次函数关系;当销售单价为70元时,销售数量为160个;当销售单价为80元时,销售数量为140个(利润率
(1)求 与 之间的函数关系式;
(2)当销售单价定为多少元时,公司每天获得利润最大,最大利润为多少元?
如图,在 中, , , ,点 , 分别在 , 上(点 与点 , 不重合),且 ,将 绕点 逆时针旋转 得到△ .当△ 的斜边、直角边与 分别相交于点 , (点 与点 不重合)时,设 , .
(1)求证: ;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.
小红在练习仰卧起坐,本月1日至4日的成绩与日期具有如下关系:
日期 |
1 |
2 |
3 |
4 |
成绩 |
40 |
43 |
46 |
49 |
小红的仰卧起坐成绩与日期
之间近似为一次函数关系,则该函数表达式为 .
为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离(单位:千米)与快递车所用时间
(单位:时)的函数图象,已知货车比快递车早1小时出发,到达武汉后用2小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚1小时.
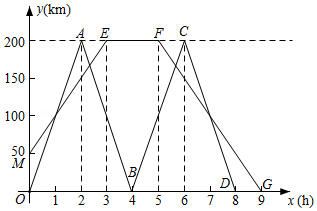
(1)求的函数解析式;
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离武汉的距离.(直接写出答案)
某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元.设第
天的销售价格为
(元
,销售量为
.该超市根据以往的销售经验得出以下的销售规律:①当
时,
;当
时,
与
满足一次函数关系,且当
时,
;
时,
.②
与
的关系为
.
(1)当时,
与
的关系式为
;
(2)为多少时,当天的销售利润
(元
最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润(元
随
的增大而增大,则需要在当天销售价格的基础上涨
元
,求
的取值范围.
如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过点 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是
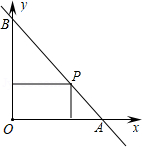
| A. |
|
B. |
|
C. |
|
D. |
|
某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该馆每间标准房的价格在元之间(含170元,240元)浮动时,每天入住的房间数
(间
与每间标准房的价格
(元
的数据如下表:
|
190 |
200 |
210 |
220 |
||
|
65 |
60 |
55 |
50 |
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
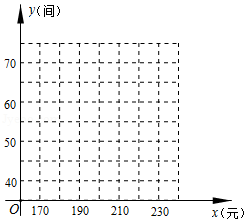
(2)求关于
的函数表达式,并写出自变量
的取值范围.
(3)设客房的日营业额为(元
.若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
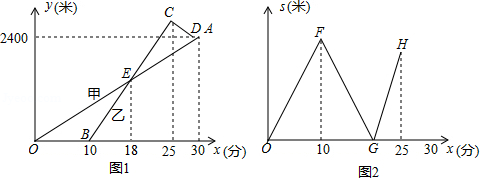
某校的甲、乙两位老师同住一小区,该小区与学校相距2400米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校又骑行若干米到达还车点后,立即步行走回学校.已知甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为(分
,图1中线段
和折线
分别表示甲、乙离开小区的路程
(米
与甲步行时间
(分
的函数关系的图象;图2表示甲、乙两人之间的距离
(米
与甲步行时间
(分
的函数关系的图象(不完整).
根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当时
关于
的函数的大致图象.(温馨提示:请画在答题卷相对应的图上)
甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元.在乙批发店,一次购买数量不超过
时,价格为7元
;一次购买数量超过
时,其中有
的价格仍为7元
,超过
部分的价格为5元
.设小王在同一个批发店一次购买苹果的数量为
.
(Ⅰ)根据题意填表:
一次购买数量 |
30 |
50 |
150 |
|
甲批发店花费 |
|
300 |
|
|
乙批发店花费 |
|
350 |
|
(Ⅱ)设在甲批发店花费元,在乙批发店花费
元,分别求
,
关于
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为 ;
②若小王在同一个批发店一次购买苹果的数量为,则他在甲、乙两个批发店中的 批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的 批发店购买数量多.
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车 辆 为非负整数),试填写表格.
表一:
| 租用甲种货车的数量 辆 |
3 |
7 |
|
| 租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
| 租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二:
| 租用甲种货车的数量 辆 |
3 |
7 |
|
| 租用甲种货车的费用 元 |
|
2800 |
|
| 租用乙种货车的费用 元 |
|
280 |
|
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
试题篮
()