初中数学一次函数的应用解答题

某校举办“创建全国文明城市”知识竞赛，计划购买甲、乙两种奖品共30件．其中甲种奖品每件30元，乙种奖品每件20元．

（1）如果购买甲、乙两种奖品共花费800元，那么这两种奖品分别购买了多少件？

（2）若购买乙种奖品的件数不超过甲种奖品件数的3倍．如何购买甲、乙两种奖品，使得总花费最少？

某汽车运输公司为了满足市场需要，推出商务车和轿车对外租赁业务．下面是乐山到成都两种车型的限载人数和单程租赁价格表：

车型	每车限载人数（人 $)$	租金（元 $/$辆）
商务车	6	300
轿车	4

（1）如果单程租赁2辆商务车和3辆轿车共需付租金1320元，求一辆轿车的单程租金为多少元？

（2）某公司准备组织34名职工从乐山赴成都参加业务培训，拟单程租用商务车或轿车前往．在不超载的情况下，怎样设计租车方案才能使所付租金最少？

某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品 $x$（吨），生产甲、乙两种产品获得的总利润为 $y$（万元）．

（1）求 $y$与 $x$之间的函数表达式；

（2）若每生产1吨甲产品需要 $A$原料0.25吨，每生产1吨乙产品需要 $A$原料0.5吨．受市场影响，该厂能获得的 $A$原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

某周日上午 $8:00$小宇从家出发，乘车1小时到达某活动中心参加实践活动． $11:00$时他在活动中心接到爸爸的电话，因急事要求他在 $12:00$前回到家，他即刻按照来活动中心时的路线，以5千米 $/$小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 $x$（小时）后，到达离家 $y$（千米）的地方，图中折线 $\mathit{OABCD}$表示 $y$与 $x$之间的函数关系．

（1）活动中心与小宇家相距　   　千米，小宇在活动中心活动时间为　 　小时，他从活动中心返家时，步行用了　    　小时；

（2）求线段 $\mathit{BC}$所表示的 $y$（千米）与 $x$（小时）之间的函数关系式（不必写出 $x$所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在 $12:00$前回到家，并说明理由．

推进农村土地集约式管理，提高土地的使用效率是新农村建设的一项重要举措．某村在小城镇建设中集约了2400亩土地，计划对其进行平整．经投标，由甲乙两个工程队来完成平整任务．甲工程队每天可平整土地45亩，乙工程队每天可平整土地30亩．已知乙工程队每天的工程费比甲工程队少500元，当甲工程队所需工程费为12000元，乙工程队所需工程费为9000元时，两工程队工作天数刚好相同．

（1）甲乙两个工程队每天各需工程费多少元？

（2）现由甲乙两个工程队共同参与土地平整，已知两个工程队工作天数均为正整数，且所有土地刚好平整完，总费用不超过110000元．

①甲乙两工程队分别工作的天数共有多少种可能？

②写出其中费用最少的一种方案，并求出最低费用．

在"新冠"疫情期间，全国人民"众志成城，同心抗疫"，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元 $/$ 件，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量 $y$ （单位：件）与线下售价 $x$ （单位：元 $/$ 件， $12⩽x<24)$ 满足一次函数的关系，部分数据如下表：

$x$ （元     $/$ 件）	12	13	14	15	16
$y$ （件     $)$	1200	1100	1000	900	800

（1）求 $y$ 与 $x$ 的函数关系式；

（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件．试问：当 $x$ 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．

某班级45名同学自发筹集到1700元资金，用于初中毕业时各项活动的经费．通过商议，决定拿出不少于544元但不超过560元的资金用于请专业人士拍照，其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品．已知每件文化衫28元，每本相册20元．

（1）设用于购买文化衫和相册的总费用为 $W$元，求总费用 $W$（元 $)$与购买的文化衫件数 $t$（件 $)$的函数关系式．

（2）购买文化衫和相册有哪几种方案？为使拍照的资金更充足，应选择哪种方案，并说明理由．

宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第 $x$天生产的产品数量为 $y$件， $y$与 $x$满足如下关系： $y=\left\{\begin{array}{c}7.5x(0⩽x⩽4)\\ 5x+10(4<x⩽14)\end{array}\right.$．

（1）工人甲第几天生产的产品数量为70件？

（2）设第 $x$天生产的产品成本为 $P$元 $/$件， $P$与 $x$的函数图象如图．工人甲第 $x$天创造的利润为 $W$元，求 $W$与 $x$的函数关系式，并求出第几天时，利润最大，最大利润是多少？

为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买2个甲种文具、1个乙种文具共需花费35元；购买1个甲种文具、3个乙种文具共需花费30元．

（1）求购买一个甲种文具、一个乙种文具各需多少元？

（2）若学校计划购买这两种文具共120个，投入资金不少于955元又不多于1000元，设购买甲种文具 $x$个，求有多少种购买方案？

（3）设学校投入资金 $W$元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？

小明放学后从学校回家，出发5分钟时，同桌小强发现小明的数学作业卷忘记拿了，立即拿着数学作业卷按照同样的路线去追赶小明，小强出发10分钟时，小明才想起没拿数学作业卷，马上以原速原路返回，在途中与小强相遇．两人离学校的路程 $y$（米 $)$与小强所用时间 $x$（分钟）之间的函数图象如图所示．

（1）求函数图象中 $a$的值；

（2）求小强的速度；

（3）求线段 $\mathit{AB}$的函数解析式，并写出自变量的取值范围．

为庆祝中华人民共和国七十周年华诞，某广场舞团队准备购买甲、乙两种道具参加演出，已知购买2件甲种道具、1件乙种道具共需35元；购买1件甲种道具、3种乙种道具共需花费30元．

（1）求购买一件甲种道具，一件乙种道具各需多少元？

（2）若该团体计划购买这两种道具共120件，投入资金不少于956元又不多于1000元，设购买甲种道具 $x$件，求有多少种购买方案？

（3）设投入资金为 $W$元，在（2）的条件下，哪种购买方案需要投入的资金最少？最少资金是多少元？

小明匀速跑步从甲地到乙地，在途中因故停留了一段时间后，仍按原速跑步，小强骑自行车比小明晚出发一段时间，以400米 $/$分的速度匀速从乙地到甲地，两人距离乙地的路程 $y$（米 $)$与小明出发后所用时间 $t$（分钟）之间的函数图象如图所示，

（1）求小明跑步的速度；

（2）求小明停留结束后 $y$与 $x$之间的函数解析式，并写出自变量的取值范围；

（3）求小明与小强相遇时 $x$的值．

端午节期间，甲、乙两人沿同一路线行驶，各自开车同时去离家560千米的景区游玩，甲先以每小时60千米的速度匀速行驶1小时，再以每小时 $m$千米的速度匀速行驶，途中休息了一段时间后，仍按照每小时 $m$千米的速度匀速行驶，两人同时到达目的地，图中折线、线段分别表示甲、乙两人所走的路程 $y_{甲}\left(\mathit{km}\right)$， $y_{乙}\left(\mathit{km}\right)$与时间 $x\left(h\right)$之间的函数关系的图象．请根据图象提供的信息，解决下列问题：

（1）图中 $E$点的坐标是　   ，题中 $m=$　　 $\mathit{km}/h$，甲在途中休息　　 $h$；

（2）求线段 $\mathit{CD}$的解析式，并写出自变量 $x$的取值范围；

（3）两人第二次相遇后，又经过多长时间两人相距 $20\mathit{km}$？

为了落实党的“精准扶贫”政策， $A$、 $B$两城决定向 $C$、 $D$两乡运送肥料以支持农村生产，已知 $A$、 $B$两城共有肥料500吨，其中 $A$城肥料比 $B$城少100吨，从 $A$城往 $C$、 $D$两乡运肥料的费用分别为20元 $/$吨和25元 $/$吨；从 $B$城往 $C$、 $D$两乡运肥料的费用分别为15元 $/$吨和24元 $/$吨．现 $C$乡需要肥料240吨， $D$乡需要肥料260吨．

（1） $A$城和 $B$城各有多少吨肥料？

（2）设从 $A$城运往 $C$乡肥料 $x$吨，总运费为 $y$元，求出最少总运费．

（3）由于更换车型，使 $A$城运往 $C$乡的运费每吨减少 $a(0<a<6)$元，这时怎样调运才能使总运费最少？

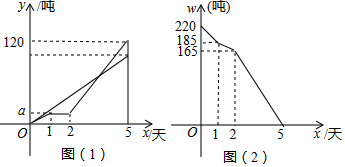
某市制米厂接到加工大米任务，要求5天内加工完220吨大米，制米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止．甲、乙两车间各自加工大米数量 $y$（吨 $)$与甲车间加工时间 $x$（天 $)$之间的关系如图（1）所示；未加工大米 $w$（吨 $)$与甲加工时间 $x$（天 $)$之间的关系如图（2）所示，请结合图象回答下列问题：

（1）甲车间每天加工大米　　吨， $a=$　　．

（2）求乙车间维修设备后，乙车间加工大米数量 $y$（吨 $)$与 $x$（天 $)$之间函数关系式．

（3）若55吨大米恰好装满一节车厢，那么加工多长时间装满第一节车厢？再加工多长时间恰好装满第二节车厢？