初中数学一次函数的应用解答题

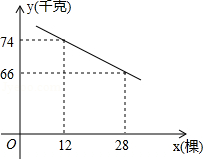
某市为节约水资源， 制定了新的居民用水收费标准， 按照新标准， 用户每月缴纳的水费 $y$（元 $)$与每月用水量 $x\left(m^3\right)$之间的关系如图所示 ．

（1） 求 $y$关于 $x$的函数解析式；

（2） 若某用户二、 三月份共用水 $40m^3$（二 月份用水量不超过 $25m^3)$，缴纳水费 79.8 元， 则该用户二、 三月份的用水量各是多少 $m^3$？

某网店销售甲、乙两种防雾霾口罩，已知甲种口罩每袋的售价比乙种口罩多5元，小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元．

（1）该网店甲、乙两种口罩每袋的售价各多少元？

（2）根据消费者需求，网店决定用不超过10000元购进甲、乙两种口罩共500袋，且甲种口罩的数量大于乙种口罩的 $\frac{4}{5}$，已知甲种口罩每袋的进价为22.4元，乙种口罩每袋的进价为18元，请你帮助网店计算有几种进货方案？若使网店获利最大，应该购进甲、乙两种口罩各多少袋，最大获利多少元？

某花店准备购进甲、乙两种花卉，若购进甲种花卉20盆，乙种花卉50盆，需要720元；若购进甲种花卉40盆，乙种花卉30盆，需要880元．

（1）求购进甲、乙两种花卉，每盆各需多少元？

（2）该花店销售甲种花卉每盆可获利6元，销售乙种花卉每盆可获利1元，现该花店准备拿出800元全部用来购进这两种花卉，设购进甲种花卉 $x$盆，全部销售后获得的利润为 $W$元，求 $W$与 $x$之间的函数关系式；

（3）在（2）的条件下，考虑到顾客需求，要求购进乙种花卉的数量不少于甲种花卉数量的6倍，且不超过甲种花卉数量的8倍，那么该花店共有几种购进方案？在所有的购进方案中，哪种方案获利最大？最大利润是多少元？

某食品连锁店研制出一种新式月饼，每块成本为6元．试销一段时间后发现，若每块月饼的售价不超过10元，每天可销售300块；若每块月饼的售价超过10元，每提高1元，每天的销量就会减少30块．这家食品连锁店每天需要支付因生产这种月饼而产生的其他费用（不含月饼成本）200元．设每块月饼的售价为 $x$（元 $)$，食品连锁店每天销售这种月饼的纯收入为 $y$（元 $)$．（注：纯收入 $=$销售额 $-$成本 $-$其他费用）

（1）当每块月饼售价不超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　．当每块月饼售价超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　　；

（2）如果这种月饼每块的售价不超过12元，那么如何定价才能使该食品连锁店每天销售这种月饼的纯收入提高？最高纯收入为多少元？

如图，在平面直角坐标系中， $\mathit{\Delta AOB}$的顶点 $O$为坐标原点，点 $A$的坐标为 $(4,0)$，点 $B$的坐标为 $(0,1)$，点 $C$为边 $\mathit{AB}$的中点，正方形 $\mathit{OBDE}$的顶点 $E$在 $x$轴的正半轴上，连接 $\mathit{CO}$， $\mathit{CD}$， $\mathit{CE}$．

（1）线段 $\mathit{OC}$的长为　　；

（2）求证： $\mathit{\Delta CBD}\cong \mathit{\Delta COE}$；

（3）将正方形 $\mathit{OBDE}$沿 $x$轴正方向平移得到正方形 $O_1{B}_1{D}_1{E}_1$，其中点 $O$， $B$， $D$， $E$的对应点分别为点 $O_1$， $B_1$， $D_1$， $E_1$，连接 $C{D}_1$， $C{E}_1$，设点 $E_1$的坐标为 $(a,0)$，其中 $a\ne 2$，△ $C{D}_1{E}_1$的面积为 $S$．

①当 $1<a<2$时，请直接写出 $S$与 $a$之间的函数表达式；

②在平移过程中，当 $S=\frac{1}{4}$时，请直接写出 $a$的值．

某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量 $y$（本 $)$与每本纪念册的售价 $x$（元 $)$之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

（1）请直接写出 $y$与 $x$的函数关系式；

（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

（3）设该文具店每周销售这种纪念册所获得的利润为 $w$元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

有一个运输队承包了一家公司运送货物的业务，第一次运送 $18t$，派了一辆大卡车和5辆小卡车；第二次运送 $38t$，派了两辆大卡车和11辆小卡车，并且两次派的车都刚好装满．

（1）两种车型的载重量各是多少？

（2）若大卡车运送一次的费用为200元，小卡车运送一次的费用为60元，在第一次运送过程中怎样安排大小车辆，才能使费用最少？（直接写出派车方案）

有一家苗圃计划植桃树和柏树，根据市场调查与预测，种植桃树的利润 $y_1$（万元）与投资成本 $x$（万元）满足如图①所示的二次函数 $y_1=a{x}^2$；种植柏树的利润 $y_2$（万元）与投资成本 $x$（万元）满足如图②所示的正比例函数 $y_2=\mathit{kx}$．

（1）分别求出利润 $y_1$（万元）和利润 $y_2$（万元）关于投资成本 $x$（万元）的函数关系式；

（2）如果这家苗圃以10万元资金投入种植桃树和柏树，桃树的投资成本不低于2万元且不高于8万元，苗圃至少获得多少利润？最多能获得多少利润？

某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果 $y$（千克），增种果树 $x$（棵 $)$，它们之间的函数关系如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？

（3）当增种果树多少棵时，果园的总产量 $w$（千克）最大？最大产量是多少？

某手工编织厂生产一种旅游纪念品，现有60名工人进行手工编织（每人编织的效率相同），2天后抽出10名工人执行其他任务，其余工人继续编织生产；2天后从编织的工人中再抽出10名进行销售（每人每天的销售量相同）．已知每人每天的销售量是编织量的5倍，下图是产品库存量 $y$（件 $)$与生产时间 $x$（天 $)$之间的函数关系图象．

（1）解释点 $B$的实际意义；

（2）求每人每天的编织量和销售量；

（3）求 $\mathit{CD}$段所在的直线的函数表达式，并求出多少天后剩余库存量低于生产前的库存量．

某超市销售樱桃，已知樱桃的进价为15元 $/$千克，如果售价为20元 $/$千克，那么每天可售出250千克，如果售价为25元 $/$千克，那么每天可获利2000元，经调查发现：每天的销售量 $y$（千克）与售价 $x$（元 $/$千克）之间存在一次函数关系．

（1）求 $y$与 $x$之间的函数关系式；

（2）若樱桃的售价不得高于28元 $/$千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？

今年是“精准扶贫”攻坚关键年，某扶贫工作队为对口扶贫村引进建立了一村集体企业，并无偿提供一笔无息贷款作为启动资金，双方约定：①企业生产出的产品全部由扶贫工作队及时联系商家收购；②企业从生产销售的利润中，要保证按时发放工人每月最低工资32000元．已知该企业生产的产品成本为20元 $/$件，月生产量 $y$（千件）与出厂价 $x$（元 $\left)\right(25⩽x⩽50)$的函数关系可用图中的线段 $\mathit{AB}$和 $\mathit{BC}$表示，其中 $\mathit{AB}$的解析式为 $y=-\frac{1}{20}x+m(m$为常数）．

（1）求该企业月生产量 $y$（千件）与出厂价 $x$（元 $)$之间的函数关系式，并写出自变量 $x$的取值范围．

（2）当该企业生产出的产品出厂价定为多少元时，月利润 $W$（元 $)$最大？最大利润是多少？ $[$月利润 $=$（出厂价 $-$成本） $\times$月生产量 $-$工人月最低工资 $]$．

某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，日销售量 $y\left(\mathit{kg}\right)$与时间第 $t$天之间的函数关系式为 $y=2t+100(1⩽t⩽80$， $t$为整数），销售单价 $p$（元 $/\mathit{kg})$与时间第 $t$天之间满足一次函数关系如下表：

时间第 $t$天	1	2	3	$\dots$	80
销售单价 $p/$（元 $/\mathit{kg})$	49.5	49	48.5	$\dots$	10

（1）直接写出销售单价 $p$（元 $/\mathit{kg})$与时间第 $t$天之间的函数关系式．

（2）在整个销售旺季的80天里，哪一天的日销售利润最大？最大利润是多少？

某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费 $y$（元）是行李质量 $x\left(\mathit{kg}\right)$的一次函数．已知行李质量为 $20\mathit{kg}$时需付行李费2元，行李质量为 $50\mathit{kg}$时需付行李费8元．

（1）当行李的质量 $x$超过规定时，求 $y$与 $x$之间的函数表达式；

（2）求旅客最多可免费携带行李的质量．

张老师计划到超市购买甲种文具100个，他到超市后发现还有乙种文具可供选择．如果调整文具的购买品种，每减少购买1个甲种文具，需增加购买2个乙种文具．设购买 $x$个甲种文具时，需购买 $y$个乙种文具．

（1）①当减少购买1个甲种文具时， $x=$　    　， $y=$　   　；

②求 $y$与 $x$之间的函数表达式．

（2）已知甲种文具每个5元，乙种文具每个3元，张老师购买这两种文具共用去540元．甲、乙两种文具各购买了多少个？