已知抛物线
与 轴交于点
轴交于点 ,与
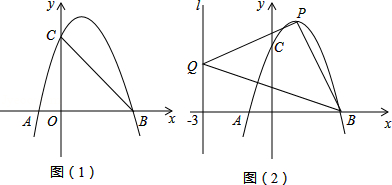
,与 轴的两个交点分别为
轴的两个交点分别为 ,
, .
.
(1)求抛物线的解析式;
(2)已知点 在抛物线上,连接
在抛物线上,连接 ,
, ,若
,若 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 的坐标;
的坐标;
(3)已知点 在
在 轴上,点
轴上,点 在抛物线上,是否存在以
在抛物线上,是否存在以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

已知,抛物线 经过原点,顶点为
经过原点,顶点为 ,
, .
.
(1)当 ,
, 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)若抛物线 也经过
也经过 点,求
点,求 与
与 之间的关系式;
之间的关系式;
(3)当点 在抛物线
在抛物线 上,且
上,且 时,求
时,求 的取值范围.
的取值范围.
如图,抛物线  经过点
经过点  ,
,  ,交
,交  轴于点
轴于点  ;
;
(1)求抛物线的解析式(用一般式表示);
(2)点  为
为  轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点  使
?若存在请直接给出点
使
?若存在请直接给出点  坐标;若不存在请说明理由;
坐标;若不存在请说明理由;
(3)将直线  绕点
绕点  顺时针旋转
顺时针旋转  ,与抛物线交于另一点
,与抛物线交于另一点  ,求
,求  的长.
的长.

如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.

如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.

如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.

如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0).

(1)求抛物线的解析式;
(2)若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由.
(注:在解题过程中,如果你觉得有困难,可以阅读下面的材料)
附阅读材料:
1.在平面直角坐标系中,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则A,B两点间的距离为 ,这个公式叫两点间距离公式.
例如:已知A,B两点的坐标分别为(﹣1,2),(2,﹣2),则A,B两点间的距离为 .
2.因式分解:x4+2x2y2+y4=(x2+y2)2.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABDE是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.

如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.

如图,抛物线 y= ax 2+2 x﹣3与 x轴交于 A、 B两点,且 B(1,0)
(1)求抛物线的解析式和点 A的坐标;
(2)如图1,点 P是直线 y= x上的动点,当直线 y= x平分∠ APB时,求点 P的坐标;
(3)如图2,已知直线 分别与 x轴、 y轴交于 C、 F两点,点 Q是直线 CF下方的抛物线上的一个动点,过点 Q作 y轴的平行线,交直线 CF于点 D,点 E在线段 CD的延长线上,连接 QE.问:以 QD为腰的等腰△ QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,连接 ,点 是线段 上的动点(与点 , 不重合),连接 并延长 交抛物线于点 ,连接 , ,设点 的横坐标为 .
(1)求抛物线的解析式和点 的坐标;
(2)当 的面积等于2时,求 的值;
(3)在点 运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.

如图1,抛物线 交 轴于 , 两点,其中点 的坐标为 ,与 轴交于点 .
(1)求抛物线的函数解析式;
(2)点 为 轴上一点,如果直线 与直线 的夹角为 ,求线段 的长度;
(3)如图2,连接 ,点 在抛物线上,且满足 ,求点 的坐标.
试题篮
()