如图,抛物线 y=ax2+bx+c(a≠0)与 x轴交于点 A(−4,0), B(2,0),与 y轴交于点 C(0,4),线段 BC的中垂线与对称轴 l交于点 D,与 x轴交于点 F,与 BC交于点 E,对称轴 l与 x轴交于点 H.
(1)求抛物线的函数表达式;
(2)求点 D的坐标;
(3)点 P为 x轴上一点, ⊙P与直线 BC相切于点 Q,与直线 DE相切于点 R.求点 P的坐标;
(4)点 M为 x轴上方抛物线上的点,在对称轴 l上是否存在一点 N,使得以点 D, P, M, N为顶点的四边形是平行四边形?若存在,则直接写出 N点坐标;若不存在,请说明理由.

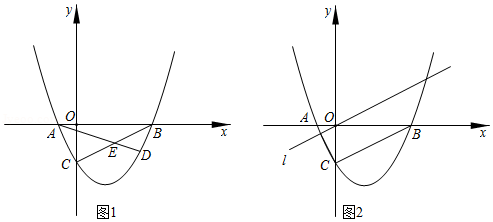
如图,在平面直角坐标系中,抛物线 y=ax2+bx+c(a≠0)与 x轴交于 A、 B两点,与 y轴交于点 C,且 OA=2, OB=8, OC=6.
(1)求抛物线的解析式;
(2)点 M从 A点出发,在线段 AB上以每秒3个单位长度的速度向 B点运动,同时,点 N从 B出发,在线段 BC上以每秒1个单位长度的速度向 C点运动,当其中一个点到达终点时,另一个点也停止运动,当 ΔMBN存在时,求运动多少秒使 ΔMBN的面积最大,最大面积是多少?
(3)在(2)的条件下, ΔMBN面积最大时,在 BC上方的抛物线上是否存在点 P,使 ΔBPC的面积是 ΔMBN面积的9倍?若存在,求点 P的坐标;若不存在,请说明理由.

在平面直角坐标系中,抛物线 y=ax2+bx+3与 x轴交于点 A(-3,0)、 B(1,0),交 y轴于点 N,点 M为抛物线的顶点,对称轴与 x轴交于点 C.
(1)求抛物线的解析式;
(2)如图1,连接 AM,点 E是线段 AM上方抛物线上一动点, EF⊥AM于点 F,过点 E作 EH⊥x轴于点 H,交 AM于点 D.点 P是 y轴上一动点,当 EF取最大值时:
①求 PD+PC的最小值;
②如图2, Q点为 y轴上一动点,请直接写出 DQ+14OQ的最小值.

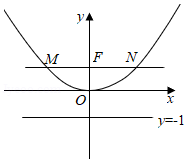
如图,已知二次函数的图象顶点在原点,且点 (2,1)在二次函数的图象上,过点 F(0,1)作 x轴的平行线交二次函数的图象于 M、 N两点.
(1)求二次函数的表达式;
(2) P为平面内一点,当 ΔPMN是等边三角形时,求点 P的坐标;
(3)在二次函数的图象上是否存在一点 E,使得以点 E为圆心的圆过点 F和点 N,且与直线 y=-1相切.若存在,求出点 E的坐标,并求 ⊙E的半径;若不存在,说明理由.
已知二次函数 y=ax2+2x+c(a≠0)的图象与 x轴的交于 A、 B(1,0)两点,与 y轴交于点 C(0,-3),
(1)求二次函数的表达式及 A点坐标;
(2) D是二次函数图象上位于第三象限内的点,求点 D到直线 AC的距离取得最大值时点 D的坐标;
(3) M是二次函数图象对称轴上的点,在二次函数图象上是否存在点 N,使以 M、 N、 B、 O为顶点的四边形是平行四边形?若有,请写出点 N的坐标(不写求解过程).

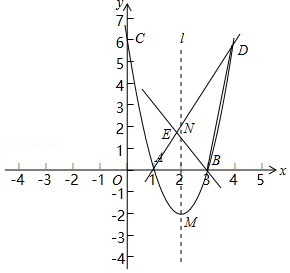
如图,抛物线 y=ax2+bx+c(a≠0)的图象经过 A(1,0), B(3,0), C(0,6)三点.
(1)求抛物线的解析式.
(2)抛物线的顶点 M与对称轴 l上的点 N关于 x轴对称,直线 AN交抛物线于点 D,直线 BE交 AD于点 E,若直线 BE将 ΔABD的面积分为 1:2两部分,求点 E的坐标.
(3) P为抛物线上的一动点, Q为对称轴上动点,抛物线上是否存在一点 P,使 A、 D、 P、 Q为顶点的四边形为平行四边形?若存在,求出点 P的坐标;若不存在,请说明理由.
如图,抛物线 y=ax2+bx+c经过 A(-1,0)、 B(4,0)、 C(0,2)三点,点 D(x,y)为抛物线上第一象限内的一个动点.
(1)求抛物线所对应的函数表达式;
(2)当 ΔBCD的面积为3时,求点 D的坐标;
(3)过点 D作 DE⊥BC,垂足为点 E,是否存在点 D,使得 ΔCDE中的某个角等于 ∠ABC的2倍?若存在,求点 D的横坐标;若不存在,请说明理由.
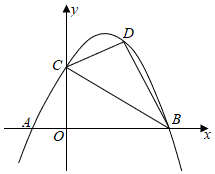
出关于 x的一元二次方程,解之取其非零值可得出点 D的横坐标.依此即可得解.
已知,抛物线 y=ax2+bx+3(a<0)与 x轴交于 A(3,0)、 B两点,与 y轴交于点 C,抛物线的对称轴是直线 x=1, D为抛物线的顶点,点 E在 y轴 C点的上方,且 CE=12.
(1)求抛物线的解析式及顶点 D的坐标;
(2)求证:直线 DE是 ΔACD外接圆的切线;
(3)在直线 AC上方的抛物线上找一点 P,使 SΔACP=12SΔACD,求点 P的坐标;
(4)在坐标轴上找一点 M,使以点 B、 C、 M为顶点的三角形与 ΔACD相似,直接写出点 M的坐标.

如图1,抛物线 y=-x2+bx+c与 x轴交于 A、 B两点,与 y轴交于点 C,已知点 B坐标为 (3,0),点 C坐标为 (0,3).

(1)求抛物线的表达式;
(2)点 P为直线 BC上方抛物线上的一个动点,当 ΔPBC的面积最大时,求点 P的坐标;
(3)如图2,点 M为该抛物线的顶点,直线 MD⊥x轴于点 D,在直线 MD上是否存在点 N,使点 N到直线 MC的距离等于点 N到点 A的距离?若存在,求出点 N的坐标;若不存在,请说明理由.
如图,已知抛物线 y=ax2+bx+c经过 A(-2,0), B(4,0), C(0,4)三点.
(1)求该抛物线的解析式;
(2)经过点 B的直线交 y轴于点 D,交线段 AC于点 E,若 BD=5DE.
①求直线 BD的解析式;
②已知点 Q在该抛物线的对称轴 l上,且纵坐标为1,点 P是该抛物线上位于第一象限的动点,且在 l右侧,点 R是直线 BD上的动点,若 ΔPQR是以点 Q为直角顶点的等腰直角三角形,求点 P的坐标.

如图,二次函数 y=ax2+bx+c的图象过 O(0,0)、 A(1,0)、 B(32, √32)三点.
(1)求二次函数的解析式;
(2)若线段 OB的垂直平分线与 y轴交于点 C,与二次函数的图象在 x轴上方的部分相交于点 D,求直线 CD的解析式;
(3)在直线 CD下方的二次函数的图象上有一动点 P,过点 P作 PQ⊥x轴,交直线 CD于 Q,当线段 PQ的长最大时,求点 P的坐标.

已知抛物线 y=ax2+bx+c与 x轴交于 A(-1,0), B(5,0)两点, C为抛物线的顶点,抛物线的对称轴交 x轴于点 D,连结 BC,且 tan∠CBD=43,如图所示.
(1)求抛物线的解析式;
(2)设 P是抛物线的对称轴上的一个动点.
①过点 P作 x轴的平行线交线段 BC于点 E,过点 E作 EF⊥PE交抛物线于点 F,连结 FB、 FC,求 ΔBCF的面积的最大值;
②连结 PB,求 35PC+PB的最小值.

如图,在平面直角坐标系 xOy中,直线 y=kx+3分别交 x轴、 y轴于 A, B两点,经过 A, B两点的抛物线 y=-x2+bx+c与 x轴的正半轴相交于点 C(1,0).
(1)求抛物线的解析式;
(2)若 P为线段 AB上一点, ∠APO=∠ACB,求 AP的长;
(3)在(2)的条件下,设 M是 y轴上一点,试问:抛物线上是否存在点 N,使得以 A, P, M, N为顶点的四边形为平行四边形?若存在,求出点 N的坐标;若不存在,请说明理由.

如图1,抛物线 y=ax2-2ax-3a(a≠0)与 x轴交于点 A, B.与 y轴交于点 C.连接 AC, BC.已知 ΔABC的面积为2.
(1)求抛物线的解析式;
(2)平行于 x轴的直线与抛物线从左到右依次交于 P, Q两点.过 P, Q向 x轴作垂线,垂足分别为 G, H.若四边形 PGHQ为正方形,求正方形的边长;
(3)如图2,平行于 y轴的直线交抛物线于点 M,交 x轴于点 N (2,0).点 D是抛物线上 A, M之间的一动点,且点 D不与 A, M重合,连接 DB交 MN于点 E.连接 AD并延长交 MN于点 F.在点 D运动过程中, 3NE+NF是否为定值?若是,求出这个定值;若不是,请说明理由.
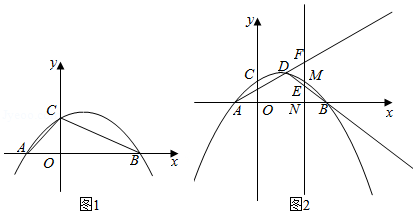
在平面直角坐标系 xOy 中,已知抛物线 y=ax2+bx+c 与 x 轴交于 A(-1,0) , B(4,0) 两点,与 y 轴交于点 C(0,-2) .
(1)求抛物线的函数表达式;
(2)如图1,点 D 为第四象限抛物线上一点,连接 AD , BC 交于点 E ,连接 BD ,记 ΔBDE 的面积为 S1 , ΔABE 的面积为 S2 ,求 S1S2 的最大值;
(3)如图2,连接 AC , BC ,过点 O 作直线 l//BC ,点 P , Q 分别为直线 l 和抛物线上的点.试探究:在第一象限是否存在这样的点 P , Q ,使 ΔPQB∽ΔCAB .若存在,请求出所有符合条件的点 P 的坐标;若不存在,请说明理由.
试题篮
()