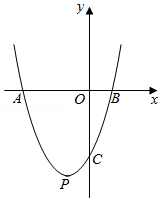
如图,抛物线 与 轴交于点 、 ,顶点为 ,对称轴为直线 ,给出下列结论:① ;②若点 的坐标为 ,则 的面积可以等于2;③ , , , 是抛物线上两点 ,若 ,则 ; ④若抛物线经过点 ,则方程 的两根为 ,3.其中正确结论的序号为 .

若抛物线 经过第四象限的点 ,则关于 的方程 的根的情况是
| A. |
有两个大于1的不相等实数根 |
| B. |
有两个小于1的不相等实数根 |
| C. |
有一个大于1另一个小于1的实数根 |
| D. |
没有实数根 |
如图,抛物线 与 轴交于点 和 ,与 轴交于点 .下列结论:① ,② ,③ ,④ ,其中正确的结论个数为

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
已知二次函数 的图象经过 与 两点,关于 的方程 有两个根,其中一个根是3.则关于 的方程 有两个整数根,这两个整数根是
| A. |
或0 |
B. |
或2 |
C. |
或3 |
D. |
或4 |
如图,已知二次函数的图象经过点
,
,与
轴交于点
.
(1)求抛物线的解析式;
(2)抛物线上是否存在点,使
,若存在请直接写出点
的坐标.若不存在,请说明理由.

如图,抛物线与
轴交于
,
两点,与
轴交于点
,抛物线的顶点为
.已知
,
.请答案下列问题:
(1)求抛物线的解析式,并直接写出点的坐标;
(2)抛物线的对称轴与轴交于点
,连接
,
的垂直平分线交直线
于点
,则线段
的长为
.
注:抛物线的对称轴是直线
,顶点坐标是
,
.
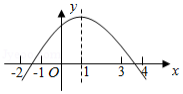
二次函数 的顶点坐标为 ,其部分图象如图所示.以下结论错误的是

| A. |
|
| B. |
|
| C. |
|
| D. |
关于 的方程 无实数根 |
如图,抛物线 的对称轴是 ,下列结论:
① ;② ;③ ;④ ,
正确的有
| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
若二次函数图象的顶点在一次函数
的图象上,则称
为
的伴随函数,如:
是
的伴随函数.
(1)若是
的伴随函数,求直线
与两坐标轴围成的三角形的面积;
(2)若函数的伴随函数
与
轴两个交点间的距离为4,求
,
的值.
如图,抛物线为常数,
与
轴交于
,
两点,点
为抛物线的顶点,点
的坐标为
,
,连接
并延长与过
,
,
三点的
相交于点
.
(1)求点的坐标;
(2)过点作
的切线
交
轴于点
.
①如图1,求证:;
②如图2,连接,
,
,当
,
时,求
的值.
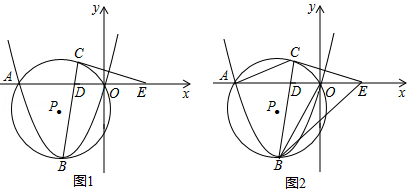
如图1,的三个顶点
、
、
分别落在抛物线
的图象上,点
的横坐标为
,点
的纵坐标为
.(点
在点
的左侧)
(1)求点、
的坐标;
(2)将绕点
逆时针旋转
得到△
,抛物线
经过
、
两点,已知点
为抛物线
的对称轴上一定点,且点
恰好在以
为直径的圆上,连接
、
,求△
的面积;
(3)如图2,延长交抛物线
于点
,连接
,在坐标轴上是否存在点
,使得以
、
、
为顶点的三角形与△
相似.若存在,请求出点
的坐标;若不存在,请说明理由.

试题篮
()