初中数学二次函数的应用试题

某商品的进价为每件40元，在销售过程中发现，每周的销售量 $y$（件 $)$与销售单价 $x$（元 $)$之间的关系可以近似看作一次函数 $y=\mathit{kx}+b$，且当售价定为50元 $/$件时，每周销售30件，当售价定为70元 $/$件时，每周销售10件．

（1）求 $k$， $b$的值；

（2）求销售该商品每周的利润 $w$（元 $)$与销售单价 $x$（元 $)$之间的函数解析式，并求出销售该商品每周可获得的最大利润．

某宾馆共有80间客房．宾馆负责人根据经验作出预测：今年7月份，每天的房间空闲数 $y$（间）与定价 $x$（元 $/$间）之间满足 $y=\frac{1}{4}x-42(x⩾168)$．若宾馆每天的日常运营成本为5000元，有客人入住的房间，宾馆每天每间另外还需支出28元的各种费用，宾馆想要获得最大利润，同时也想让客人得到实惠，应将房间定价确定为 $($　　 $)$

A．252元 $/$间B．256元 $/$间C．258元 $/$间D．260元 $/$间

超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加 $x$元，每天售出 $y$件．

（1）请写出 $y$与 $x$之间的函数表达式；

（2）当 $x$为多少时，超市每天销售这种玩具可获利润2250元？

（3）设超市每天销售这种玩具可获利 $w$元，当 $x$为多少时 $w$最大，最大值是多少？

已知矩形 $\mathit{ABCD}$中， $\mathit{AB}=5\mathit{cm}$，点 $P$为对角线 $\mathit{AC}$上的一点，且 $\mathit{AP}=2\sqrt{5}\mathit{cm}$．如图①，动点 $M$从点 $A$出发，在矩形边上沿着 $A\to B\to C$的方向匀速运动（不包含点 $C$）.设动点 $M$的运动时间为 $t\left(s\right)$， $\mathit{\Delta APM}$的面积为 $S\left(c{m}^2\right)$， $S$与 $t$的函数关系如图②所示．

（1）直接写出动点 $M$的运动速度为　    　 $\mathit{cm}/s$， $\mathit{BC}$的长度为　 　 $\mathit{cm}$；

（2）如图③，动点 $M$重新从点 $A$出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点 $N$从点 $D$出发，在矩形边上沿着 $D\to C\to B$的方向匀速运动，设动点 $N$的运动速度为 $v(\mathit{cm}/s)$．已知两动点 $M$， $N$经过时间 $x\left(s\right)$在线段 $\mathit{BC}$上相遇（不包含点 $C$），动点 $M$， $N$相遇后立即同时停止运动，记此时 $\mathit{\Delta APM}$与 $\mathit{\Delta DPN}$的面积分别为 $S_1\left(c{m}^2\right)$， $S_2\left(c{m}^2\right)$

①求动点 $N$运动速度 $v(\mathit{cm}/s)$的取值范围；

②试探究 $S_1·S_2$是否存在最大值，若存在，求出 $S_1·S_2$的最大值并确定运动时间 $x$的值；若不存在，请说明理由．

如图是王阿姨晚饭后步行的路程 $S$（单位： $m)$与时间 $t$（单位： $\mathit{min})$的函数图象，其中曲线段 $\mathit{AB}$是以 $B$为顶点的抛物线一部分．下列说法不正确的是 $($　　 $)$

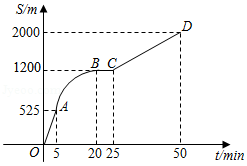
A． $25\mathit{min}~50\mathit{min}$，王阿姨步行的路程为 $800m$

B．线段 $\mathit{CD}$的函数解析式为 $S=32t+400(25⩽t⩽50)$

C． $5\mathit{min}~20\mathit{min}$，王阿姨步行速度由慢到快

D．曲线段 $\mathit{AB}$的函数解析式为 $S=-3{(t-20)}^2+1200(5⩽t⩽20)$

如图，利用一个直角墙角修建一个梯形储料场 $\mathit{ABCD}$，其中 $\angle C=120°$．若新建墙 $\mathit{BC}$与 $\mathit{CD}$总长为 $12m$，则该梯形储料场 $\mathit{ABCD}$的最大面积是 $($　　 $)$

A． $18m^2$B． $18\sqrt{3}{m}^2$C． $24\sqrt{3}{m}^2$D． $\frac{45\sqrt{3}}{2}{m}^2$

如图，在边长为 $6\mathit{cm}$的正方形 $\mathit{ABCD}$中，点 $E$、 $F$、 $G$、 $H$分别从点 $A$、 $B$、 $C$、 $D$同时出发，均以 $1\mathit{cm}/s$的速度向点 $B$、 $C$、 $D$、 $A$匀速运动，当点 $E$到达点 $B$时，四个点同时停止运动，在运动过程中，当运动时间为　     　 $s$时，四边形 $\mathit{EFGH}$的面积最小，其最小值是　     　 $c{m}^2$．

在"新冠"疫情期间，全国人民"众志成城，同心抗疫"，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元 $/$ 件，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量 $y$ （单位：件）与线下售价 $x$ （单位：元 $/$ 件， $12⩽x<24)$ 满足一次函数的关系，部分数据如下表：

$x$ （元     $/$ 件）	12	13	14	15	16
$y$ （件     $)$	1200	1100	1000	900	800

（1）求 $y$ 与 $x$ 的函数关系式；

（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件．试问：当 $x$ 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．

某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为 $x$元 $(x$为正整数），每个月的销售利润为 $y$元．

（1）当每件商品的售价是多少元时，每个月的利润刚好是2250元？

（2）当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第 $x$天生产的产品数量为 $y$件， $y$与 $x$满足如下关系： $y=\left\{\begin{array}{c}7.5x(0⩽x⩽4)\\ 5x+10(4<x⩽14)\end{array}\right.$．

（1）工人甲第几天生产的产品数量为70件？

（2）设第 $x$天生产的产品成本为 $P$元 $/$件， $P$与 $x$的函数图象如图．工人甲第 $x$天创造的利润为 $W$元，求 $W$与 $x$的函数关系式，并求出第几天时，利润最大，最大利润是多少？

随着地铁和共享单车的发展，“地铁 $+$单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的 $A$， $B$， $C$， $D$， $E$中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为 $x$（单位：千米），乘坐地铁的时间 $y_1$（单位：分钟）是关于 $x$的一次函数，其关系如下表：

地铁站	$A$	$B$	$C$	$D$	$E$
$x$（千米）	8	9	10	11.5	13
$y_1$（分钟）	18	20	22	25	28

（1）求 $y_1$关于 $x$的函数表达式；

（2）李华骑单车的时间（单位：分钟）也受 $x$的影响，其关系可以用 $y_2=\frac{1}{2}{x}^2-11x+78$来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle A=90°$． $\mathit{AB}=8\mathit{cm}$， $\mathit{AC}=6\mathit{cm}$，若动点 $D$从 $B$出发，沿线段 $\mathit{BA}$运动到点 $A$为止（不考虑 $D$与 $B$， $A$重合的情况），运动速度为 $2\mathit{cm}/s$，过点 $D$作 $\mathit{DE}//\mathit{BC}$交 $\mathit{AC}$于点 $E$，连接 $\mathit{BE}$，设动点 $D$运动的时间为 $x\left(s\right)$， $\mathit{AE}$的长为 $y\left(\mathit{cm}\right)$．

（1）求 $y$关于 $x$的函数表达式，并写出自变量 $x$的取值范围；

（2）当 $x$为何值时， $\mathit{\Delta BDE}$的面积 $S$有最大值？最大值为多少？

如图，在平面直角坐标系中，菱形 $\mathit{ABCD}$的边 $\mathit{AB}$在 $x$轴上，点 $B$坐标 $(-3,0)$，点 $C$在 $y$轴正半轴上，且 $\sin \angle \mathit{CBO}=\frac{4}{5}$，点 $P$从原点 $O$出发，以每秒一个单位长度的速度沿 $x$轴正方向移动，移动时间为 $t(0⩽t⩽5)$秒，过点 $P$作平行于 $y$轴的直线 $l$，直线 $l$扫过四边形 $\mathit{OCDA}$的面积为 $S$．

（1）求点 $D$坐标．

（2）求 $S$关于 $t$的函数关系式．

（3）在直线 $l$移动过程中， $l$上是否存在一点 $Q$，使以 $B$、 $C$、 $Q$为顶点的三角形是等腰直角三角形？若存在，直接写出 $Q$点的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，菱形 $\mathit{ABCD}$的边 $\mathit{AB}$在 $x$轴上，点 $B$坐标 $(-3,0)$，点 $C$在 $y$轴正半轴上，且 $\sin \angle \mathit{CBO}=\frac{4}{5}$，点 $P$从原点 $O$出发，以每秒一个单位长度的速度沿 $x$轴正方向移动，移动时间为 $t(0⩽t⩽5)$秒，过点 $P$作平行于 $y$轴的直线 $l$，直线 $l$扫过四边形 $\mathit{OCDA}$的面积为 $S$．

（1）求点 $D$坐标．

（2）求 $S$关于 $t$的函数关系式．

（3）在直线 $l$移动过程中， $l$上是否存在一点 $Q$，使以 $B$、 $C$、 $Q$为顶点的三角形是等腰直角三角形？若存在，直接写出 $Q$点的坐标；若不存在，请说明理由．

某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入．已知某种土特产每袋成本10元．试销阶段每袋的销售价 $x$（元 $)$与该土特产的日销售量 $y$（袋 $)$之间的关系如表：

$x$（元 $)$	15	20	30	$\dots$
$y$（袋 $)$	25	20	10	$\dots$

若日销售量 $y$是销售价 $x$的一次函数，试求：

（1）日销售量 $y$（袋 $)$与销售价 $x$（元 $)$的函数关系式；

（2）假设后续销售情况与试销阶段效果相同，要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？