如图,在菱形中,
为对角线,点
,
分别在
,
上,
,连接
.
(1)求证:;
(2)延长交
的延长线于点
,连接
交
于点
.若
,
,求
的长.

如图1, 是 的直径,直线 与 相切于点 ,直线 与 相切于点 ,点 (异于点 在 上,点 在 上,且 ,延长 与 相交于点 ,连接 并延长交 于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,连接 并延长与 分别相交于点 、 ,连接 .若 , ,求 .
(1)如图1,在中,
,以点
为中心,把
逆时针旋转
,得到△
;再以点
为中心,把
顺时针旋转
,得到△
,连接
,则
与
的位置关系为 ;
(2)如图2,当是锐角三角形,
时,将
按照(1)中的方式旋转
,连接
,探究
与
的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接,若
,△
的面积为4,则△
的面积为 .

如图,在中,
,
是
上一点,
经过点
、
、
,交
于点
,过点
作
,交
于点
.
求证:(1)四边形是平行四边形;
(2).

在一副三角板ABC和DEF中,
(1)当AB∥CD,如图①。求∠DCB的度数。
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由。
(3)如图③,当∠DCB等于多少度时,AB∥EC?


如图,的半径
,过点
作
的切线
,且
,连接
并延长,与
交于点
、
,过点
作
,并与
交于点
,连接
、
.
(1)求证:;
(2)求的长.

(本题6分)如图,在△ABC中,点E在BC上,CD⊥AB, EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
在等腰 中, ,以 为直径的 分别与 , 相交于点 , ,过点 作 ,垂足为点 .
(1)求证: 是 的切线;
(2)分别延长 , ,相交于点 , , 的半径为6,求阴影部分的面积.

(本题6分)AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是:________________.
∴BE∥DF.
理由是:________________.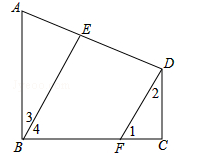
试题篮
()