初中数学全等三角形的判定与性质试题

如图，在△ABC中，∠C=90°，AC=BC=2，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，下列结论：

①△DFE是等腰直角三角形；
②四边形CEDF的周长不变；
③点C到线段EF的最大距离为1．
其中正确的结论有__________（填写所有正确结论的序号）

如图，已知线段与相交于点，联结，为的中点，为的中点，联结．若∠A=∠D，∠OEF=∠OFE，求证：AB=DC．

如图，P为等腰△ABC的顶角A的外角平分线上任一点，连接PB，PC．

（1）求证：PB+PC＞2AB．
（2）当PC=2，PB=，∠ACP=45°时，求AB的长．

已知：如图，点在同一直线上，，，∥．求证：．

数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：

小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
①李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________．
②小聪的作法正确吗？请说明理由．
③请你帮小颖设计用刻度尺作角平分线的方法．（要求：作出图形，写出作图步骤，不予证明）

两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，小明在探究筝形的性质时，得到如下结论：

①AC⊥BD；②AO=CO=AC；③△ABD≌△CBD，其中正确的结论有（  ）

A．①②

B．①③

C．②③

D．①②③

如图，在ΔABC与ΔDCB 中，AC与BD 交于点E，且，∠A=∠D，AB=DC．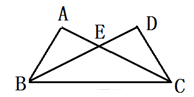

（1）求证：ΔABE≌ΔDCE
（2）当∠AEB=70°时，求∠EBC的度数．

如图，已知D是BC的中点，过点D作BC的垂线交∠A的平分线于点E，EF⊥AB于点F，EG⊥AC于点G．求证：BF=CG．

雨伞的中截面如图所示，伞骨AB＝AC，支撑杆OE＝OF，AE＝AB，AF＝AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．

如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据计算图中实线所围成的图形的面积S= ___________．

如图，等腰，，，于点，点是延长线上一点，点是线段上一点，，下面结论：
①；
②是等边三角形；
③；
④．
其中正确的是（  ）

A．②③

B．①②④

C．③④

D．①②③④

画图、证明：如图，∠AOB=90°，点C、D分别在OA、OB上．

（1）尺规作图（不写作法，保留作图痕迹）：
作∠AOB的平分线OP；作线段CD的垂直平分线EF，分别与CD、OP相交于E、F；连接OE、CF、DF．
（2）在所画图中，线段OE与CD之间有怎样的数量关系，线段DF与CF之间有怎样的数量关系，并说明理由．

如图，已知点P为∠AOB的角平分线上的一点，点D在边OA上．爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OB上取一点E，使得PE=PD，这时他发现∠OEP与∠ODP之间有一定的数量关系，请你写出∠OEP与∠ODP所有可能的数量关系是     ．     

如图，点D在BC上，DE垂直平分AC，垂足为E，F是BA的中点．

求证：DF是AB的垂直平分线．

（年贵州省贵阳市）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O于点D，连接OD交BC于点E，∠B=30°，FO=．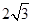

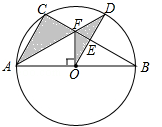
（1）求AC的长度；
（2）求图中阴影部分的面积．（计算结果保留根号）