证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证,并写出证明过程.

如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )

A.1B.2C.3D.4
如图,在Rt△ ABC中,∠ C=90°,∠ B=30°,以 A为圆心适当长为半径画弧,分别交 AB、 AC于点 M、 N,分别以点 M、 N为圆心,大于 MN的长为半径画弧交于点 P,作射线 AP交 BC于点 D,再作射线 DE交 AB于点 E,则下列结论错误的是( )

| A. |
∠ADB=120° |
B. |
S △ ADC:S △ ABC=1:3 |
| C. |
若CD=2,则BD=4 |
D. |
DE垂直平分AB |
如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)

如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 .(写出所有正确结论的序号)

如图, 中, , 为 的角平分线,以点 为圆心, 为半径作 与线段 交于点 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.

如图1,已知点 在四边形 的边 上,且 , 平分 ,与 交于点 , 分别与 、 交于点 、 .
(1)求证: ;
(2)如图2,若 ,求 的值;
(3)当四边形 的周长取最大值时,求 的值.

如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交 、 于点 、 .
②分别以点 、 为圆心,大于 的同样长为半径作弧,两弧交于点 .
③作射线 交 于点 .
如果 , , 的面积为18,则 的面积为 .

如图,已知 是锐角三角形 .
(1)请在图1中用无刻度的直尺和圆规作图:作直线 ,使 上的各点到 、 两点的距离相等;设直线 与 、 分别交于点 、 ,作一个圆,使得圆心 在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 , ,则 的半径为 .

如图,已知线段 ,点 在平面直角坐标系 内.
(1)用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)
(2)在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.
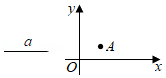
如图,在 中, 为直径,点 为圆上一点,延长 到点 ,使 ,且 .
(1)求证: 是 的切线.
(2)分别过 、 两点作直线 的垂线,垂足分别为 、 两点,过 点作 的垂线,垂足为点 .求证: .

如图, 中, , 的平分线交 于 , 交 的延长线于点 , 交 于点 .
(1)若 ,求 的度数;
(2)若 ,求 的长.
试题篮
()