初中数学等腰三角形的性质试题

如图，在中，，以为直径的分别与，交于点，，过点作，垂足为点．

（1）求证：直线是的切线；

（2）求证：；

（3）若的半径为4，，求阴影部分的面积．

已知抛物线 $y=x^2-1$ 与 $y$ 轴交于点 $A$ ，与直线 $y=\mathit{kx}(k$ 为任意实数）相交于 $B$ ， $C$ 两点，则下列结论不正确的是 $($ 　　 $)$

A．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 为等腰三角形
B．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 的内角中有两角分别为 $30°$ 和 $60°$
C．	任意实数 $k$ ，使得 $\mathit{\Delta ABC}$ 都为直角三角形
D．	存在实数 $k$ ，使得 $\mathit{\Delta ABC}$ 为等边三角形

如图，已知是的直径，，是的弦，交于，过点作的切线交的延长线于点，连接并延长交的延长线于点．

（1）求证：是的切线；

（2）若，，求线段的长．

如图， $\mathit{AB}//\mathit{CD}$ ， $\mathit{AD}=\mathit{CD}$ ， $\angle 1=50°$ ，则 $\angle 2$ 的度数是 $($ 　　 $)$

A．

$55°$

B．

$60°$

C．

$65°$

D．

$70°$

一个等腰三角形的底边长是6，腰长是一元二次方程 $x^2-8x+15=0$ 的一根，则此三角形的周长是 $($ 　　 $)$

A．

16

B．

12

C．

14

D．

12或16

如图，在四边形中，，点是的中点，．求证：．

如图，等腰 $\mathit{\Delta ABC}$ 的内切圆 $\odot O$ 与 $\mathit{AB}$ ， $\mathit{BC}$ ， $\mathit{CA}$ 分别相切于点 $D$ ， $E$ ， $F$ ，且 $\mathit{AB}=\mathit{AC}=5$ ， $\mathit{BC}=6$ ，则 $\mathit{DE}$ 的长是 $($ 　　 $)$

A．

$\frac{3\sqrt{10}}{10}$

B．

$\frac{3\sqrt{10}}{5}$

C．

$\frac{3\sqrt{5}}{5}$

D．

$\frac{6\sqrt{5}}{5}$

如图，正五边形中，对角线与相交于点，则　　度．

等腰三角形的两边长分别为，，其周长为　　．

如图，是的外接圆，的平分线交于点，交于点，过点作直线．

（1）判断直线与的位置关系，并说明理由；

（2）若，，，求的长．

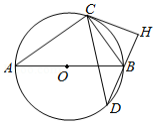
如图，为的直径，，为圆上的两点，，弦，相交于点．

（1）求证：；

（2）若，，求的半径；

（3）在（2）的条件下，过点作的切线，交的延长线于点，过点作交于，两点（点在线段上），求的长．

如图，在中，，点，都在边上，，若，则的长为　　．

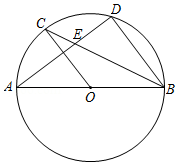
如图，为的直径，为上的一点，，，的延长线交于点，连接．

（1）求证：是的切线；

（2）若为的中点，求的值．

我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于，可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．

（1）已知凸五边形的各条边都相等．

①如图1，若，求证：五边形是正五边形；

②如图2，若，请判断五边形是不是正五边形，并说明理由：

（2）判断下列命题的真假．（在括号内填写“真”或“假”

如图3，已知凸六边形的各条边都相等．

①若，则六边形是正六边形；　　

②若，则六边形是正六边形．　　

如图，在等腰中，，以为直径作交于点，过点作，垂足为．

（1）求证：是的切线．

（2）若，，求的长．