(1)计算: (-1)2-(π-2021)0+|-12| ;
(2)如图,在 ΔABC 中, ∠A=40° , ∠ABC=80° , BE 平分 ∠ABC 交 AC 于点 E , ED⊥AB 于点 D ,求证: AD=BD .
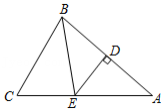
小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形, ∠ACB 与 ∠ECD 恰好为对顶角, ∠ABC=∠CDE=90° ,连接 BD , AB=BD ,点 F 是线段 CE 上一点.
探究发现:
(1)当点 F 为线段 CE 的中点时,连接 DF (如图(2) ) ,小明经过探究,得到结论: BD⊥DF .你认为此结论是否成立? .(填"是"或"否" )
拓展延伸:
(2)将(1)中的条件与结论互换,即: BD⊥DF ,则点 F 为线段 CE 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若 AB=6 , CE=9 ,求 AD 的长.

如图1,四边形 ABCD 的对角线 AC , BD 相交于点 O , OA=OC , OB=OD+CD .
(1)过点 A 作 AE//DC 交 BD 于点 E ,求证: AE=BE ;
(2)如图2,将 ΔABD 沿 AB 翻折得到 ΔABD' .
①求证: ;
②若 ,求证: .

如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
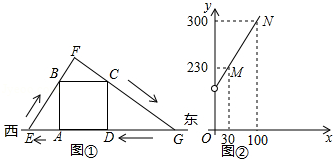
如图①,直线 表示一条东西走向的笔直公路,四边形 是一块边长为100米的正方形草地,点 , 在直线 上,小明从点 出发,沿公路 向西走了若干米后到达点 处,然后转身沿射线 方向走到点 处,接着又改变方向沿射线 方向走到公路 上的点 处,最后沿公路 回到点 处.设 米(其中 , 米,已知 与 之间的函数关系如图②所示,
(1)求图②中线段 所在直线的函数表达式;
(2)试问小明从起点 出发直至最后回到点 处,所走过的路径(即 是否可以是一个等腰三角形?如果可以,求出相应 的值;如果不可以,说明理由.
在菱形 中, ,点 是射线 上一动点,以 为边向右侧作等边 ,点 的位置随着点 的位置变化而变化.

(1)如图1,当点 在菱形 内部或边上时,连接 , 与 的数量关系是 , 与 的位置关系是 ;
(2)当点 在菱形 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图4,当点 在线段 的延长线上时,连接 ,若 , ,求四边形 的面积.
已知, 中, , 是 边上一点,作 ,分别交边 , 于点 , .
(1)若 (如图 ,求证: .
(2)若 ,过点 作 ,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就 情形(如图 说明理由.
(3)若点 与 重合(如图 , ,且 .
①求 的度数;
②设 , , ,试证明: .

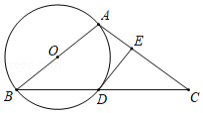
如图,在 中, ,以 为直径的 交 于点 ,切线 交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

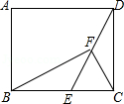
如图,矩形 中,点 为 上一点, 为 的中点,且 .
(1)当 为 中点时,求证: ;
(2)当 时,求 的值;
(3)设 , ,作点 关于 的对称点 ,连接 , ,若点 到 的距离是 ,求 的值.
如图, 中, , ,点 , 分别在 , 上, ,点 为 的延长线与 的延长线的交点.
(1)求证: ;
(2)判断 和 的数量关系,并说明理由;
(3)若 , ,求 的长.

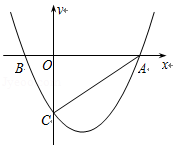
如图,抛物线 与 轴交于 、 两点,与 轴交于 点,已知 ,且 是抛物线上另一点.
(1)求 、 的值;
(2)连接 ,设点 是 轴上任一点,若以 、 、 三点为顶点的三角形是等腰三角形,求 点的坐标;
(3)若点 是 轴正半轴上且在抛物线内的一动点(不与 、 重合),过点 作 交抛物线的对称轴于 点.设 , 的面积为 ,求 与 之间的函数关系式.
如图,已知 , 分别为 的边 , 上两点,点 , , 在 上,点 , 在 上. 为 上一点,连接 并延长交 的延长线于点 ,交 于点 .
(1)若 为 ,请将 用含 的代数式表示;
(2)若 ,请说明当 为多少度时,直线 为 的切线;
(3)在(2)的条件下,若 ,求 的值.
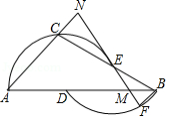
如图,已知 是 的直径,点 是圆上异于 、 的一点,连结 并延长至点 ,使 ,连结 交 于点 ,连结 .
(1)求证: 是等腰三角形;
(2)连结 并延长,与以 为切点的切线交于点 ,若 , ,求 的长.

试题篮
()