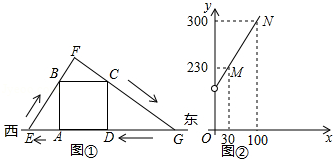
如图①,直线 表示一条东西走向的笔直公路,四边形 是一块边长为100米的正方形草地,点 , 在直线 上,小明从点 出发,沿公路 向西走了若干米后到达点 处,然后转身沿射线 方向走到点 处,接着又改变方向沿射线 方向走到公路 上的点 处,最后沿公路 回到点 处.设 米(其中 , 米,已知 与 之间的函数关系如图②所示,
(1)求图②中线段 所在直线的函数表达式;
(2)试问小明从起点 出发直至最后回到点 处,所走过的路径(即 是否可以是一个等腰三角形?如果可以,求出相应 的值;如果不可以,说明理由.
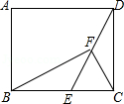
已知, 中, , 是 边上一点,作 ,分别交边 , 于点 , .
(1)若 (如图 ,求证: .
(2)若 ,过点 作 ,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就 情形(如图 说明理由.
(3)若点 与 重合(如图 , ,且 .
①求 的度数;
②设 , , ,试证明: .

如图,矩形 中,点 为 上一点, 为 的中点,且 .
(1)当 为 中点时,求证: ;
(2)当 时,求 的值;
(3)设 , ,作点 关于 的对称点 ,连接 , ,若点 到 的距离是 ,求 的值.
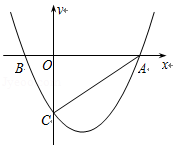
如图,抛物线 与 轴交于 、 两点,与 轴交于 点,已知 ,且 是抛物线上另一点.
(1)求 、 的值;
(2)连接 ,设点 是 轴上任一点,若以 、 、 三点为顶点的三角形是等腰三角形,求 点的坐标;
(3)若点 是 轴正半轴上且在抛物线内的一动点(不与 、 重合),过点 作 交抛物线的对称轴于 点.设 , 的面积为 ,求 与 之间的函数关系式.
已知抛物线 的顶点为 ,与 轴的交点为 .
(1)求 的解析式;
(2)若直线 与 仅有唯一的交点,求 的值;
(3)若抛物线 关于 轴对称的抛物线记作 ,平行于 轴的直线记作 .试结合图形回答:当 为何值时, 与 和 共有:①两个交点;②三个交点;③四个交点;
(4)若 与 轴正半轴交点记作 ,试在 轴上求点 ,使 为等腰三角形.

已知抛物线经过点
和
,与
轴交于另一点
,顶点为
.
(1)求抛物线的解析式,并写出点的坐标;
(2)如图,点,
分别在线段
,
上
点不与
,
重合),且
,则
能否为等腰三角形?若能,求出
的长;若不能,请说明理由;
(3)若点在抛物线上,且
,试确定满足条件的点
的个数.

如图1,经过等边
的顶点
,
(圆心
在
内),分别与
,
的延长线交于点
,
,连结
,
交
于点
.
(1)求证:.
(2)当,
时,求
的长.
(3)设,
.
①求关于
的函数表达式;
②如图2,连结,
,若
的面积是
面积的10倍,求
的值.

如图,在平面直角坐标系中,抛物线与
轴交于
、
两点(点
在点
的左侧),与
轴交于点
,对称轴与
轴交于点
,点
在抛物线上.

(1)求直线的解析式;
(2)点为直线
下方抛物线上的一点,连接
,
.当
的面积最大时,连接
,
,点
是线段
的中点,点
是
上的一点,点
是
上的一点,求
的最小值;
(3)点是线段
的中点,将抛物线
沿
轴正方向平移得到新抛物线
,
经过点
,
的顶点为点
.在新抛物线
的对称轴上,是否存在点
,使得
为等腰三角形?若存在,直接写出点
的坐标;若不存在,请说明理由.
综合与探究
如图,在平面直角坐标系中,已知抛物线 与 轴交于 , 两点,与 轴交于点 ,直线 经过坐标原点 ,与抛物线的一个交点为 ,与抛物线的对称轴交于点 ,连接 ,已知点 , 的坐标分别为 , .
(1)求抛物线的函数表达式,并分别求出点 和点 的坐标;
(2)试探究抛物线上是否存在点 ,使 ?若存在,请直接写出点 的坐标;若不存在,请说明理由;
(3)若点 是 轴负半轴上的一个动点,设其坐标为 ,直线 与直线 交于点 ,试探究:当 为何值时, 是等腰三角形.

试题篮
()