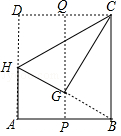
如图,在一张矩形纸片 ABCD中, AB=3,点 P, Q分别是 AB和 CD的中点,现将这张纸片折叠,使点 D落到 PQ上的点 G处,折痕为 CH,若 HG的延长线恰好经过点 B,则 AD的长为 .
如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若 ,∠EFA=60°,则四边形A′B′EF的周长是( )

A.1+3 B.3+ C.4+ D.5+
如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6;④S△OCF=2S△OEF
:6;④S△OCF=2S△OEF
成立的个数有( )

A.1个B.2个C.3个D.4个
(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.
①请按要求画图:将 绕点 顺时针方向旋转 ,点 的对应点为点 ,点 的对应点为点 .连接 ;
②在①中所画图形中, .
(2)【问题解决】
如图2,在 中, , ,延长 到 ,使 ,将斜边 绕点 顺时针旋转 到 ,连接 ,求 的度数.
(3)【拓展延伸】
如图3,在四边形 中, ,垂足为 , , , , 为常数),求 的长(用含 的式子表示).

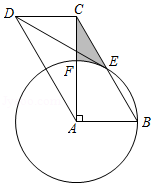
如图,在平行四边形 中, 是对角线, ,以点 为圆心,以 的长为半径作 ,交 边于点 ,交 于点 ,连接 .
(1)求证: 与 相切;
(2)若 , ,求阴影部分的面积.
【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .


(1)如图①,点 在 上,点 在 上, , .求证: .
(2)如图②, 为 上一点,按以下步骤作图:
①连接 ;
②以点 为圆心, 长为半径作弧,交 于点 ;
③在射线 上截取 ;
④连接 .
若 ,求 的半径.

如图,是
的弦,
是
外一点,
,
交
于点
,交
于点
,且
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,求图中阴影部分的面积.
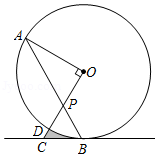
如图, 为半圆 的直径, , 是半圆上的三等分点, , 与半圆 相切于点 .点 为 上一动点(不与点 , 重合),直线 交 于点 , 于点 ,延长 交 于点 ,则下列结论正确的是 .(写出所有正确结论的序号)
① ;② 的长为 ;③ ;④ ;⑤ 为定值.

如图, 内接于 , 是 的直径.直线 与 相切于点 ,在 上取一点 使得 ,线段 , 的延长线交于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留 .

如图,在四边形 中, , , ,过点 的 与边 , 分别交于 , 两点. ,垂足为 , .连接 , , .

(1)若 ,试判断 的形状,并说明理由;
(2)若 ,求证: 与 相切于点 .
定义:有一组对角互余的四边形叫做对余四边形.
理解:
(1)若四边形 是对余四边形,则 与 的度数之和为 ;
证明:
(2)如图1, 是 的直径,点 , , 在 上, , 相交于点 .
求证:四边形 是对余四边形;
探究:
(3)如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由.

试题篮
()