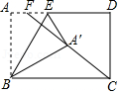
如图,矩形 中, , ,点 为 上一点,且 ,将 沿 翻折,得到△ ,连接 并延长,与 相交于点 ,则 的长为 .
现有 、 两个大型储油罐,它们相距 ,计划修建一条笔直的输油管道,使得 、 两个储油罐到输油管道所在直线的距离都为 ,输油管道所在直线符合上述要求的设计方案有 种.
如图,在 中, , 是 上一点, ,点 是射线 上的一个动点, ,则当 为直角三角形时, 的长为 .

四边形具有不稳定性.如图,矩形 按箭头方向变形成平行四边形 ,当变形后图形面积是原图形面积的一半时,则 .

如图,矩形 , ,以点 为圆心,以任意长为半径作弧分别交 , 于点 , 两点,再分别以点 , 为圆心,以大于 的长作半径作弧交于点 ,作射线 交 于点 ,若 ,则矩形 的面积等于 .

如图,在四边形ABCD中,对角线AC、BD相交于点E, , , , ,则AE= (提示:可过点A作BD的垂线)

如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP= .

如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形 的对角线 , 相交于点 .以点 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则 的长为 (结果保留 .

数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形中,
,
.如图,建立平面直角坐标系
,使得边
在
轴正半轴上,点
在
轴正半轴上,则点
的坐标是 .

如图,在平面直角坐标系中,菱形的顶点
为坐标原点,顶点
在
轴的正半轴上,顶点
在反比例函数
的图象上,已知菱形的周长是8,
,则
的值是 .

试题篮
()