已知菱形 的面积为 ,点 是一边 上的中点,点 是对角线 上的动点.连接 ,若 平分 ,则线段 与 的和的最小值为 ,最大值为 .
如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
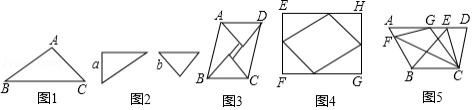
某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积 , , 之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在 中, 为斜边,分别以 , , 为斜边向外侧作 , , ,若 ,则面积 , , 之间的关系式为 ;
推广验证
(2)如图3,在 中, 为斜边,分别以 , , 为边向外侧作任意 , , ,满足 , ,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形 中, , , , ,点 在 上, , ,求五边形 的面积.

如图,在四边形 中,对角线 与 交于点 ,已知 , ,过点 作 ,分别交 、 于点 , ,连接 , .
(1)求证:四边形 是菱形:
(2)设 , , ,求 的长.
如图,在 中, , , , 为 边上的一个动点,连接 , 为 上的一个动点,连接 , ,当 时,线段 的最小值是

| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
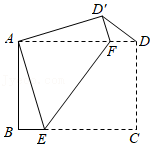
如图,将等腰直角三角形纸片 对折,折痕为 .展平后,再将点 折叠在边 上(不与 、 重合),折痕为 ,点 在 上的对应点为 ,设 与 交于点 ,连接 .已知 .
(1)若 为 的中点,求 的长;
(2)随着点 在边 上取不同的位置,
① 的形状是否发生变化?请说明理由;
②求 的周长的取值范围.

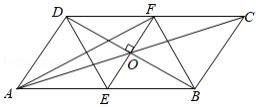
如图,在正方形 中, , 为边 上的两个三等分点,点 关于 的对称点为 , 的延长线交 于点 .
(1)求证: ;
(2)求 的大小;
(3)求证: .
抛物线与
轴交于点
,
(点
在点
的左边),与
轴交于点
,点
是该抛物线的顶点.
(1)如图1,连接,求线段
的长;
(2)如图2,点是直线
上方抛物线上一点,
轴于点
,
与线段
交于点
;将线段
沿
轴左右平移,线段
的对应线段是
,当
的值最大时,求四边形
周长的最小值,并求出对应的点
的坐标;
(3)如图3,点是线段
的中点,连接
,将
沿直线
翻折至△
的位置,再将△
绕点
旋转一周,在旋转过程中,点
,
的对应点分别是点
,
,直线
分别与直线
,
轴交于点
,
.那么,在△
的整个旋转过程中,是否存在恰当的位置,使
是以
为腰的等腰三角形?若存在,请直接写出所有符合条件的线段
的长;若不存在,请说明理由.

(回顾)
如图1, 中, , , ,则 的面积等于 .
(探究)
图2是同学们熟悉的一副三角尺,一个含有 的角,较短的直角边长为 ;另一个含有 的角,直角边长为 ,小明用两副这样的三角尺拼成一个平行四边形 (如图 ,用了两种不同的方法计算它的面积,从而推出 ,小丽用两副这样的三角尺拼成了一个矩形 (如图 ,也推出 ,请你写出小明或小丽推出 的具体说理过程.
(应用)
在四边形 中, , , , , (如图5)
(1)点 在 上,设 ,求 的最小值;
(2)点 在 上,将 沿 翻折,点 落在 上的点 处,点 是 的中点吗?说明理由.
如图,已知线段 , 于点 ,且 , 是射线 上一动点, , 分别是 , 的中点,过点 , , 的圆与 的另一交点 (点 在线段 上),连接 , .
(1)当 时,求 和 的度数;
(2)求证: .
(3)在点 的运动过程中
①当 时,取四边形 一边的两端点和线段 上一点 ,若以这三点为顶点的三角形是直角三角形,且 为锐角顶点,求所有满足条件的 的值;
②记 与圆的另一个交点为 ,将点 绕点 旋转 得到点 ,当点 恰好落在 上时,连接 , , , ,直接写出 和 的面积之比.

在一次数学探究活动中,李老师设计了一份活动单:
已知线段 ,使用作图工具作 ,尝试操作后思考: (1)这样的点 唯一吗? (2)点 的位置有什么特征?你有什么感悟? |
“追梦”学习小组通过操作、观察、讨论后汇报:点 的位置不唯一,它在以 为弦的圆弧上(点 、 除外), .小华同学画出了符合要求的一条圆弧(如图 .
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
② 面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你根据图1证明 .
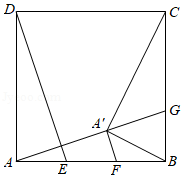
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点 在直线 的左侧,且 .
①线段 长的最小值为 ;
②若 ,则线段 长为 .

问题提出
(1)如图①,在中,
,
,则
的外接圆半径
的值为 .
问题探究
(2)如图②,的半径为13,弦
,
是
的中点,
是
上一动点,求
的最大值.
问题解决
(3)如图③所示,、
、
是某新区的三条规划路,其中
,
,
,
所对的圆心角为
,新区管委会想在
路边建物资总站点
,在
,
路边分别建物资分站点
、
,也就是,分别在
、线段
和
上选取点
、
、
.由于总站工作人员每天都要将物资在各物资站点间按
的路径进行运输,因此,要在各物资站点之间规划道路
、
和
.为了快捷、环保和节约成本.要使得线段
、
、
之和最短,试求
的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
如图1,在 中, , ,点 是 边上一点(含端点 、 ,过点 作 垂直于射线 ,垂足为 ,点 在射线 上,且 ,连接 、 .

(1)求证: ;
(2)如图2,连接 ,点 、 、 分别为线段 、 、 的中点,连接 、 、 .求 的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.
试题篮
()