(1)【探究发现】
如图1,∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处,∠ EOF=90°,将∠ EOF绕点 O旋转,旋转过程中,∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F(点 F与点 C, D不重合).则 CE, CF, BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的"正方形 ABCD"改为"∠ BCD=120°的菱形 ABCD",其他条件不变,当∠ EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3,∠ BOD=120°, OD= , OB=4, OA平分∠ BOD, AB= ,且 OB>2 OA,点 C是 OB上一点,∠ CAD=60°,求 OC的长.

如图,已知 A、 F、 C、 D四点在同一条直线上, AF= CD, AB∥ DE,且 AB= DE.
(1)求证:△ ABC≌△ DEF;
(2)若 EF=3, DE=4,∠ DEF=90°,请直接写出使四边形 EFBC为菱形时 AF的长度.

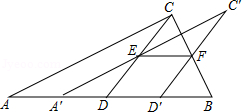
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.

如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知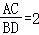 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .


如图,在平面直角坐标系中,点 为坐标原点,菱形 的顶点 的坐标为 .
(1)求过点 的反比例函数 的解析式;
(2)连接 ,过点 作 交 轴于点 ,求直线 的解析式.

定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形 中, , ,过点 作 垂线交 的延长线于点 ,且 ,证明:四边形 是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形 内接于 中, .求 的半径.

如图1,正方形和
的边
,
在同一条直线上,且
,取
的中点
,连接
,
,
.
(1)试证明,并求
的值.
(2)如图2,将图1中的正方形变为菱形,设,其它条件不变,问(1)中
的值有变化吗?若有变化,求出该值(用含
的式子表示);若无变化,说明理由.

如图,是菱形
的对角线,
,
(1)请用尺规作图法,作的垂直平分线
,垂足为
,交
于
;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接,求
的度数.

如图1,菱形的顶点
,
在直线上,
,以点
为旋转中心将菱形
顺时针旋转
,得到菱形
,
交对角线
于点
,
交直线
于点
,连接
.
(1)当时,求
的大小.
(2)如图2,对角线交
于点
,交直线
与点
,延长
交
于点
,连接
.当
的周长为2时,求菱形
的周长.

试题篮
()