初中数学矩形的性质试题

将矩形 $\mathit{ABCD}$纸片按如图所示的方式折叠， $\mathit{EF}$， $\mathit{EG}$为折痕，试问 $\angle \mathit{AEF}+\angle \mathit{BEG}=$　　．

如图，矩形 $\mathit{ABCD}$绕点 $B$逆时针旋转 $30°$后得到矩形 $A_{1}B{C}_1{D}_1$， $C_1{D}_1$与 $\mathit{AD}$交于点 $M$，延长 $\mathit{DA}$交 $A_1{D}_1$于 $F$，若 $\mathit{AB}=1$， $\mathit{BC}=\sqrt{3}$，则 $\mathit{AF}$的长度为 $($　　 $)$

A． $2-\sqrt{3}$B． $\frac{\sqrt{3}-1}{3}$C． $\frac{3-\sqrt{3}}{3}$D． $\sqrt{3}-1$

如图，矩形 $\mathit{ABCD}$的对角线 $\mathit{AC}$的中点为 $O$，过点 $O$作 $\mathit{OE}\perp \mathit{BC}$于点 $E$，连接 $\mathit{OD}$，已知 $\mathit{AB}=6$， $\mathit{BC}=8$，则四边形 $\mathit{OECD}$的周长为　　．

如图，在平面直角坐标系 $\mathit{xOy}$中，矩形 $\mathit{OABC}$的边 $\mathit{OA}$、 $\mathit{OC}$分别在 $x$轴和 $y$轴上， $\mathit{OC}=3$， $\mathit{OA}=2\sqrt{6}$， $D$是 $\mathit{BC}$的中点，将 $\mathit{\Delta OCD}$沿直线 $\mathit{OD}$折叠后得到 $\mathit{\Delta OGD}$，延长 $\mathit{OG}$交 $\mathit{AB}$于点 $E$，连接 $\mathit{DE}$，则点 $G$的坐标为　　．

（2） $\because \tan \angle \mathit{ACB}=\frac{\mathit{AB}}{\mathit{BC}}=\frac{\sqrt{2}}{2}$， $\mathit{BC}=2$，

$\therefore \mathit{AB}=\mathit{BC}·\tan \angle \mathit{ACB}=\sqrt{2}$，

$\therefore \mathit{AC}=\sqrt{6}$；

又 $\because \angle \mathit{ACB}=\angle \mathit{DCE}$，

$\therefore \tan \angle \mathit{DCE}=\tan \angle \mathit{ACB}=\frac{\sqrt{2}}{2}$，

$\therefore \mathit{DE}=\mathit{DC}·\tan \angle \mathit{DCE}=1$；

方法一：在 $\text{Rt}\Delta \text{CDE}$中， $\mathit{CE}=\sqrt{C{D}^2+D{E}^2}=\sqrt{3}$，

连接 $\mathit{OE}$，设 $\odot O$的半径为 $r$，则在 $\text{Rt}\Delta \text{COE}$中， $C{O}^2=O{E}^2+C{E}^2$，即 ${(\sqrt{6}-r)}^2=r^2+3$

解得： $r=\frac{\sqrt{6}}{4}$

方法二： $\mathit{AE}=\mathit{AD}-\mathit{DE}=1$，过点 $O$作 $\mathit{OM}\perp \mathit{AE}$于点 $M$，则 $\mathit{AM}=\frac{1}{2}\mathit{AE}=\frac{1}{2}$

在 $\text{Rt}\Delta \text{AMO}$中， $\mathit{OA}=\frac{\mathit{AM}}{\cos \angle \mathit{EAO}}=\frac{1}{2}÷\frac{2}{\sqrt{6}}=\frac{\sqrt{6}}{4}$

本题考查了圆的综合题：圆的切线垂直于过切点的半径；利用勾股定理计算线段的长．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AD}=4$， $\angle \mathit{DAC}=30°$，点 $P$、 $E$分别在 $\mathit{AC}$、 $\mathit{AD}$上，则 $\mathit{PE}+\mathit{PD}$的最小值是 $($　　 $)$

A．2B． $2\sqrt{3}$C．4D． $\frac{8\sqrt{3}}{3}$

如图，矩形 $\mathit{ABCD}$的边 $\mathit{BC}$在 $x$轴上，点 $A$在第二象限，点 $D$在第一象限， $\mathit{AB}=2\sqrt{3}$， $\mathit{OD}=4$，将矩形 $\mathit{ABCD}$绕点 $O$旋转，使点 $D$落在 $x$轴上，则点 $C$对应点的坐标是 $($　　 $)$

A． $(-\sqrt{3}$， $1)$B． $(-1,\sqrt{3})$

C． $(-1,\sqrt{3})$或 $(1,-\sqrt{3})$D． $(-\sqrt{3}$， $1)$或 $(1,-\sqrt{3})$

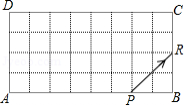
如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=8$， $\mathit{BC}=4$，一发光电子开始置于 $\mathit{AB}$边的点 $P$处，并设定此时为发光电子第一次与矩形的边碰撞，将发光电子沿着 $\mathit{PR}$方向发射，碰撞到矩形的边时均反射，每次反射的反射角和入射角都等于 $45°$，若发光电子与矩形的边碰撞次数经过2019次后，则它与 $\mathit{AB}$边的碰撞次数是　　．

如图，在矩形 $\mathit{ABCD}$中， $E$， $F$分别是 $\mathit{BC}$， $\mathit{AD}$边上的点，且 $\mathit{AE}=\mathit{CF}$．

（1）求证： $\mathit{\Delta ABE}\cong \mathit{\Delta CDF}$；

（2）当 $\mathit{AC}\perp \mathit{EF}$时，四边形 $\mathit{AECF}$是菱形吗？请说明理由．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=\sqrt{3}$， $\mathit{AD}=3$，点 $P$是 $\mathit{AD}$边上的一个动点，连接 $\mathit{BP}$，作点 $A$关于直线 $\mathit{BP}$的对称点 $A_1$，连接 $A_{1}C$，设 $A_{1}C$的中点为 $Q$，当点 $P$从点 $A$出发，沿边 $\mathit{AD}$运动到点 $D$时停止运动，点 $Q$的运动路径长为　　．

如图，在矩形 $\mathit{ABCD}$中，以 $\mathit{BC}$边为直径作半圆 $O$， $\mathit{OE}\perp \mathit{OA}$交 $\mathit{CD}$边于点 $E$，对角线 $\mathit{AC}$与半圆 $O$的另一个交点为 $P$，连接 $\mathit{AE}$．

（1）求证： $\mathit{AE}$是半圆 $O$的切线；

（2）若 $\mathit{PA}=2$， $\mathit{PC}=4$，求 $\mathit{AE}$的长．

（1）如图1，在正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{AE}\perp \mathit{BF}$于点 $M$，求证： $\mathit{AE}=\mathit{BF}$；

（2）如图2，将 （1）中的正方形 $\mathit{ABCD}$改为矩形 $\mathit{ABCD}$， $\mathit{AB}=2$， $\mathit{BC}=3$， $\mathit{AE}\perp \mathit{BF}$于点 $M$，探究 $\mathit{AE}$与 $\mathit{BF}$的数量关系，并证明你的结论．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=\sqrt{2}$， $E$是 $\mathit{BC}$的中点， $\mathit{AE}\perp \mathit{BD}$于点 $F$，则 $\mathit{CF}$的长是　　．

如图，在矩形 $\mathit{ABCD}$中，对角线 $\mathit{AC}$， $\mathit{BD}$交于点 $O$，过点 $A$作 $\mathit{EA}\perp \mathit{CA}$交 $\mathit{DB}$的延长线于点 $E$，若 $\mathit{AB}=3$， $\mathit{BC}=4$，则 $\frac{\mathit{AO}}{\mathit{AE}}$的值为　　．

如图，矩形 $\mathit{ABCD}$的对角线 $\mathit{AC}$， $\mathit{BD}$相交于点 $O$，点 $E$， $F$在 $\mathit{BD}$上， $\mathit{BE}=\mathit{DF}$．

（1）求证： $\mathit{AE}=\mathit{CF}$；

（2）若 $\mathit{AB}=6$， $\angle \mathit{COD}=60°$，求矩形 $\mathit{ABCD}$的面积．