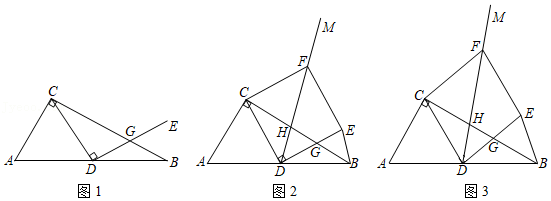
如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
如图,在矩形 中, 是边 上一点, , ,垂足为 .将四边形 绕点 顺时针旋转 ,得到四边形 , 所在的直线分别交直线 于点 ,交直线 于点 ,交 于点 . 所在的直线分别交直线 于点 ,交直线 于点 ,连接 交 于点 .
(1)如图1,求证:四边形 是正方形;
(2)如图2,当点 和点 重合时.
①求证: ;
②若 , ,求线段 的长;
(3)如图3,若 交 于点 , ,求 的值.

如图,在直角坐标系中, 的直角边 在 轴上, , ,反比例函数 的图象经过 边的中点 .
(1)求这个反比例函数的表达式;
(2)若 与 成中心对称,且 的边 在 轴的正半轴上,点 在这个函数的图象上.
①求 的长;
②连接 , ,证明四边形 是正方形.

已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .
(1)求证: ;
(2)当 与 满足什么关系时,四边形 是正方形?请说明理由.
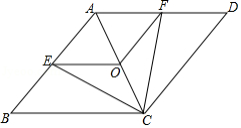
在菱形 中,点 为对角线 上一点,点 , 在直线 上,且 , .
(1)如图1,求证: ;
(2)如图2,当 时,求证: ;
(3)如图3,当 ,点 在线段 上时,线段 , , 的数量关系如何?(请直接写出你猜想的结论)
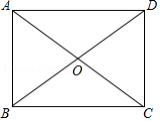
如图所示,已知平行四边形 ,对角线 , 相交于点 , .
(1)求证:平行四边形 是矩形;
(2)请添加一个条件使矩形 为正方形.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,试判断四边形 的形状,并证明你的结论.

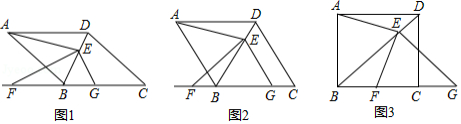
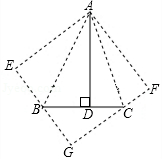
如图,在△ ABC中,∠ BAC=45°, AD⊥ BC于点 D, BD=6, DC=4,求 AD的长.小明同学利用翻折,巧妙地解答了此题,按小明的思路探究并解答下列问题:
(1)分别以 AB, AC所在直线为对称轴,画出△ ABD和△ ACD的对称图形,点 D的对称点分别为点 E, F,延长 EB和 FC相交于点 G,求证:四边形 AEGF是正方形;
(2)设 AD= x,建立关于 x的方程模型,求出 AD的长.
实践操作:
第一步:如图1,将矩形纸片 沿过点 的直线折叠,使点 落在 上的点 处,得到折痕 ,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片 沿过点 的直线折叠,点 恰好落在 上的点 处,点 落在点 处,得到折痕 , 交 于点 , 交 于点 ,再把纸片展平.
问题解决:
(1)如图1,填空:四边形 的形状是 ;
(2)如图2,线段 与 是否相等?若相等,请给出证明;若不等,请说明理由;
(3)如图2,若 , ,求 的值.

已知抛物线过点
,
两点,与
轴交于点
,
.
(1)求抛物线的解析式及顶点的坐标;
(2)过点作
,垂足为
,求证:四边形
为正方形;
(3)点为抛物线在直线
下方图形上的一动点,当
面积最大时,求点
的坐标;
(4)若点为线段
上的一动点,问:
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.

小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若
,
,求正方形
的边长(用
,
表示).
(2)操作:如何画出这个正方形呢?
如图2,小波画出了图1的,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在
上任取一点
,画正方形
,使点
,
在
边上,点
在
内,然后连结
,并延长交
于点
,画
于点
,
交
于点
,
于点
,得到四边形
.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:小波把图2中的线段称为“波利亚线”,在该线上截取
,连结
,
(如图
,当
时,求“波利亚线”
的长(用
,
表示).
请帮助小波解决“温故”、“推理”、“拓展”中的问题.

如图,在中,
,点
在对角线
上,
,
于点
,
的延长线交
于点
.点
在
的延长线上,且
,连接
.
(1)若,
,求
的长;
(2)求证:.

试题篮
()