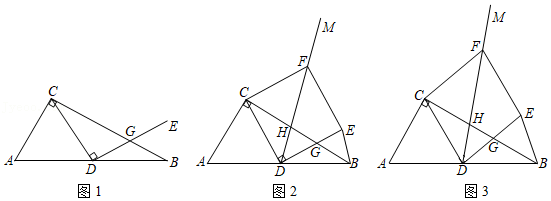
如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
如图,在矩形 中, 是边 上一点, , ,垂足为 .将四边形 绕点 顺时针旋转 ,得到四边形 , 所在的直线分别交直线 于点 ,交直线 于点 ,交 于点 . 所在的直线分别交直线 于点 ,交直线 于点 ,连接 交 于点 .
(1)如图1,求证:四边形 是正方形;
(2)如图2,当点 和点 重合时.
①求证: ;
②若 , ,求线段 的长;
(3)如图3,若 交 于点 , ,求 的值.

已知抛物线过点
,
两点,与
轴交于点
,
.
(1)求抛物线的解析式及顶点的坐标;
(2)过点作
,垂足为
,求证:四边形
为正方形;
(3)点为抛物线在直线
下方图形上的一动点,当
面积最大时,求点
的坐标;
(4)若点为线段
上的一动点,问:
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.

小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若
,
,求正方形
的边长(用
,
表示).
(2)操作:如何画出这个正方形呢?
如图2,小波画出了图1的,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在
上任取一点
,画正方形
,使点
,
在
边上,点
在
内,然后连结
,并延长交
于点
,画
于点
,
交
于点
,
于点
,得到四边形
.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:小波把图2中的线段称为“波利亚线”,在该线上截取
,连结
,
(如图
,当
时,求“波利亚线”
的长(用
,
表示).
请帮助小波解决“温故”、“推理”、“拓展”中的问题.

试题篮
()