如图所示,梯形 中, , , , , ,点 是边 上的动点,点 是射线 上一点,射线 和射线 交于点 ,且 .
(1)求线段 的长;
(2)如果 是以 为腰的等腰三角形,求线段 的长;
(3)如果点 在边 上(不与点 、 重合),设 , ,求 关于 的函数解析式,并写出 的取值范围.

问题提出:
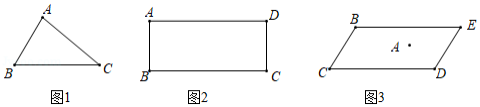
(1)如图1,已知 ,试确定一点 ,使得以 , , , 为顶点的四边形为平行四边形,请画出这个平行四边形;
问题探究:
(2)如图2,在矩形 中, , ,若要在该矩形中作出一个面积最大的 ,且使 ,求满足条件的点 到点 的距离;
问题解决:
(3)如图3,有一座塔 ,按规定,要以塔 为对称中心,建一个面积尽可能大的形状为平行四边形的景区 .根据实际情况,要求顶点 是定点,点 到塔 的距离为50米, ,那么,是否可以建一个满足要求的面积最大的平行四边形景区 ?若可以,求出满足要求的平行四边形 的最大面积;若不可以,请说明理由.(塔 的占地面积忽略不计)
问题提出
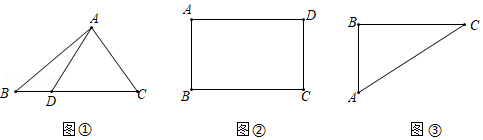
(1)如图①,已知直线 及 外一点 ,试在直线 上确定 、 两点,使 ,并画出这个 .
问题探究
(2)如图②, 是边长为28的正方形 的对称中心, 是 边上的中点,连接 .试在正方形 的边上确定点 ,使线段 和 将正方形 分割成面积之比为 的两部分.求点 到点 的距离.
问题解决
(3)如图③,有一个矩形花园 , , .根据设计要求,点 、 在对角线 上,且 ,并在四边形区域 内种植一种红色花卉,在矩形内其他区域均种植一种黄色花卉.已知种植这种红色花卉每平方米需210元,种植这种黄色花卉每平方米需180元.试求按设计要求,完成这两种花卉的种植至少需费用多少元?(结果保留整数.参考数据: ,

问题提出
(1)如图①,在 中, , 为 上一点, ,则 面积的最大值是 .
问题探究
(2)如图②,已知矩形 的周长为12,求矩形 面积的最大值.
问题解决
(3)如图③, 是葛叔叔家的菜地示意图,其中 米, 米, 米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形 ,且满足 .你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
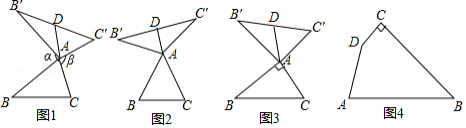
我们定义:如图1,在 中,把 绕点 顺时针旋转 得到 ,把 绕点 逆时针旋转 得到 ,连接 .当 时,我们称△ 是 的“旋补三角形”,△ 边 上的中线 叫做 的“旋补中线”,点 叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△ 是 的“旋补三角形”, 是 的“旋补中线”.
①如图2,当 为等边三角形时, 与 的数量关系为 ;
②如图3,当 , 时,则 长为 .
猜想论证:
(2)在图1中,当 为任意三角形时,猜想 与 的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形 , , , , , .在四边形内部是否存在点 ,使 是 的“旋补三角形”?若存在,给予证明,并求 的“旋补中线”长;若不存在,说明理由.
试题篮
()