已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.

如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .
(1)如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为 .
(2)如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形 的边长为6, , ,请直接写出线段 的长.
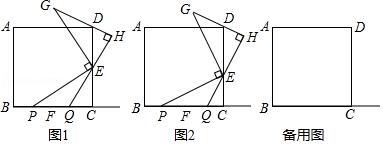
如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

如图,四边形 是正方形,连接 ,将 绕点 逆时针旋转 得 ,连接 , 为 的中点,连接 , .
(1)如图1,当 时,请直接写出 与 的关系(不用证明).
(2)如图2,当 时,(1)中的结论是否成立?请说明理由.
(3)当 时,若 ,请直接写出点 经过的路径长.

如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知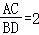 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 .(写出所有正确结论的序号)

定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形 , , ,
①若 , ,求对角线 的长.
②若 ,求证: ,
(2)如图2,在矩形 中, , ,点 是对角线 上一点,且 ,过点 作直线分别交边 , 于点 , ,使四边形 是等腰直角四边形,求 的长.

(1)如图①,在四边形 中, ,点 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.
解决此问题可以用如下方法:延长 交 的延长线于点 ,易证 得到 ,从而把 , , 转化在一个三角形中即可判断.
, , 之间的等量关系 ;
(2)问题探究:如图②,在四边形 中, , 与 的延长线交于点 ,点 是 的中点,若 是 的平分线,试探究 , , 之间的等量关系,并证明你的结论.
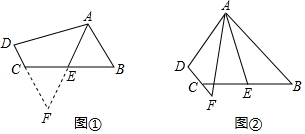
如图1,以 的较短边 为一边作菱形 ,使点 落在边 上,连接 ,交 于点 .
(1)猜想 与 的数量关系,并说明理由;
(2)延长 、 交于点 ,其他条件不变:
①如图2,若 ,求 的值;
②如图3,若
,直接写出
的值(用含
的三角函数表示)
如图,矩形  的对角线
的对角线  ,
,  相交于点
相交于点  ,
,  关于
关于  的对称图形为
的对称图形为  .
.
(1)求证:四边形  是菱形;
是菱形;
(2)连接  ,若
,若  ,
,  .
.
①求  的值;
的值;
②若点  为线段
为线段  上一动点(不与点
上一动点(不与点  重合),连接
重合),连接  ,一动点
,一动点  从点
从点  出发,以
出发,以  的速度沿线段
的速度沿线段  匀速运动到点
匀速运动到点  ,再以
,再以  的速度沿线段
的速度沿线段  匀速运动到点
匀速运动到点  ,到达点
,到达点  后停止运动,当点
后停止运动,当点  沿上述路线运动到点
沿上述路线运动到点  所需要的时间最短时,求
所需要的时间最短时,求  的长和点
的长和点  走完全程所需的时间.
走完全程所需的时间.

菱形 中、 ,点 为射线 上的动点,作射线 与直线 相交于点 ,将射线 绕点 逆时针旋转 ,得到射线 ,射线 与直线 相交于点 .
(1)如图①,点 与点 重合时,点 , 分别在线段 , 上,请直接写出 , , 三条段段之间的数量关系;
(2)如图②,点 在 的延长线上,且 , , 分别在线段 的延长线和线段 的延长线上,请写出 , , 三条线段之间的数量关系,并说明理由;
(3)点 在线段 上,若 , ,当 时,请直接写出 的长.

如图,平面直角坐标系中  是原点,
是原点,  的顶点
的顶点  ,
,  的坐标分别是
的坐标分别是  ,
,  ,点
,点  ,
,  把线段
把线段  三等分,延长
三等分,延长  、
、  分别交
分别交  、
、  于点
于点  ,
,  ,连接
,连接  .则下列结论:
.则下列结论:
①  是
是  的中点;②
的中点;②  与
与  相似;③四边形
相似;③四边形  的面积是
;④
的面积是
;④
其中正确的结论是 (填写所有正确结论的序号).

请完成如下探究系列的有关问题:
探究1:如图1, 是等腰直角三角形, ,点 为 上一动点,连接 ,以 为边在 的右侧作正方形 ,连接 ,则线段 , 之间的位置关系为 ,数量关系为 .
探究2:如图2,当点 运动到线段 的延长线上,其余条件不变,探究1中的两条结论是否仍然成立?为什么?(请写出证明过程)
探究3:如图3,如果 , , 仍然保留为 ,点 在线段 上运动,请你判断线段 , 之间的位置关系,并说明理由.

如图1, ,分别在 的两边 , 上取点 , ,使 ,点 在 的平分线 上, 于点 ,点 在线段 上(不与点 重合),以 , 为邻边作 ,连接 , .
(1)猜想 与 之间的关系,并证明你的猜想;
(2)如图2,连接 交 于点 .
①求证: .
②若 , ,求线段 的长.

试题篮
()