初中数学圆内接四边形的性质试题

如图1，小明将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=5，AD=4．在进行如下操作时遇到了下面的几个问题，请你帮助解决．

（1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时，EF恰好经过点A（如图2），请你求出AE和FG的长度．
（2）在（1）的条件下，小明先将三角形的边EG和矩形边AB重合，然后将△EFG沿直线BC向右平移，至F点与B重合时停止．在平移过程中，设G点平移的距离为x，两纸片重叠部分面积为y，求在平移的整个过程中，y与x的函数关系式，并求当重叠部分面积为10时，平移距离x的值（如图3）．
（3）在（2）的操作中，小明发现在平移过程中，虽然有时平移的距离不等，但两纸片重叠的面积却是相等的；而有时候平移的距离不等，两纸片重叠部分的面积也不可能相等．请探索这两种情况下重叠部分面积y的范围（直接写出结果）．

如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．

（1）求∠EAF的度数；
（2）如图2，连接FC交BD于M，交AD于N．
①求证：AD=AF+2DM；
②若AF=10，AN=12，则MD的长为  ．

下列图形都是由同样大小的矩形按一定规律组成，其中第（1）个图形的面积为2，第（2）个图形的面积为8，第（3）个图形的面积为18，……，则第（10）个图形的面积为（    ）

A．196

B．200

C．216

D．256

（本小题7分）如图1，已知是等腰直角三角形，，点是的中点．作
正方形，使点、分别在和上，连接 ，．

（1）试猜想线段和的数量关系是          并证明．
（2）将正方形绕点逆时针方向旋转，判断（1）中的结论是否仍然成立？请利用图2证明你的结论；

如图，四边形ABCD是边长为1的正方形，且DE＝，△ABF是△ADE的旋转图形

（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）AF的长度是多少？
（4）如果连结EF，那么△AEF是怎样的三角形？

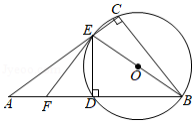
如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle C=90°$ ， $\mathit{AB}$ 的垂直平分线分别交 $\mathit{AB}$ 、 $\mathit{AC}$ 于点 $D$ 、 $E$ ， $\mathit{BE}=8$ ， $\odot O$ 为 $\mathit{\Delta BCE}$ 的外接圆，过点 $E$ 作 $\odot O$ 的切线 $\mathit{EF}$ 交 $\mathit{AB}$ 于点 $F$ ，则下列结论正确的是 　　 $.$ （写出所有正确结论的序号）

① $\mathit{AE}=\mathit{BC}$ ；

② $\angle \mathit{AED}=\angle \mathit{CBD}$ ；

③若 $\angle \mathit{DBE}=40°$ ，则 $\widehat{\mathit{DE}}$ 的长为 $\frac{8\pi }{9}$ ；

④ $\frac{\mathit{DF}}{\mathit{EF}}=\frac{\mathit{EF}}{\mathit{BF}}$ ；

⑤若 $\mathit{EF}=6$ ，则 $\mathit{CE}=2.24$ ．

正方形ABCD中，将一个直角三角板的直角顶点与点A重合，一条直角边与边BC交于点E（点E不与点B和点C重合），另一条直角边与边CD的延长线交于点F.

（1）如图①，求证：AE="AF;"
（2）如图②，此直角三角板有一个角是45°，它的斜边MN与边CD交于G，且点G是斜边MN的中点，连接EG，求证：EG="BE+DG;"
（3）在（2）的条件下，如果= ，那么点G是否一定是边CD的中点?请说明你的理由.

如图，正方形ABCD中，点E，F分别在边AB，BC上，AF=DE，AF和DE相交于点G．

（1）观察图形，写出图中所有与∠AED相等的角．
（2）选择图中与∠AED相等的任意一个角，并加以证明．

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ，分别过点 $B$ ， $C$ 作 $\angle \mathit{BAC}$ 平分线的垂线，垂足分别为点 $D$ ， $E$ ， $\mathit{BC}$ 的中点是 $M$ ，连接 $\mathit{CD}$ ， $\mathit{MD}$ ， $\mathit{ME}$ ．则下列结论错误的是 $($ 　　 $)$

A．

$\mathit{CD}=2\mathit{ME}$

B．

$\mathit{ME}//\mathit{AB}$

C．

$\mathit{BD}=\mathit{CD}$

D．

$\mathit{ME}=\mathit{MD}$

如图，在锐角三角形 $\mathit{ABC}$中， $\mathit{AD}$是 $\mathit{BC}$边上的高，以 $\mathit{AD}$为直径的 $\odot O$交 $\mathit{AB}$于点 $E$，交 $\mathit{AC}$于点 $F$，过点 $F$作 $\mathit{FG}\perp \mathit{AB}$，垂足为 $H$，交 $\stackrel{̂}{\mathit{AE}}$于点 $G$，交 $\mathit{AD}$于点 $M$，连接 $\mathit{AG}$， $\mathit{DE}$， $\mathit{DF}$．

（1）求证： $\angle \mathit{GAD}+\angle \mathit{EDF}=180°$；

（2）若 $\angle \mathit{ACB}=45°$， $\mathit{AD}=4$， $\tan \angle \mathit{ABC}=2$，求 $\mathit{HF}$的长．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．

如图所示，已知△ABC中，AC=BC=6，∠C=90°．O是AB的中点，⊙O与AC相切于点D、与BC相切于点E．设⊙O交OB于F，连DF并延长交CB的延长线于G．

（1）∠BFG与∠BGF是否相等?为什么?
（2）求由DG、GE和所围成的图形的面积（阴影部分）．

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（   ）

A．3

B．4

C．5

D．6

已知菱形ABCD边长为5cm，tan∠DAB=,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F。若点P为AD上一点，且∠DPE+∠DAB=90⁰,则AP长为          ．