如图,在斜边为3的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…依次作下去,则第2014个正方形A2014B2014C2014D2014的边长是( )
A. |
B. |
C. |
D. |
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )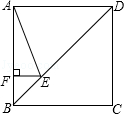
| A.1 | B.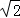 |
C.4﹣2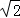 |
D.3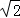 ﹣4 ﹣4 |
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
A.10 B.12 C.14 D.16
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
| A.甲正确,乙错误 | B.乙正确,甲错误 |
| C.甲、乙均正确 | D.甲、乙均错误 |
如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
A.22 B.20 C.18 D.16
如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合),以BD、BF为邻边作平行四边形BDEF,又AP綊BE(点P、E在直线AB的同侧),如果BD= AB,那么△PBC的面积与△ABC的面积之比为( )
AB,那么△PBC的面积与△ABC的面积之比为( )
A. B.
B. C.
C. D.
D.
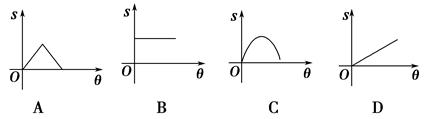
如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )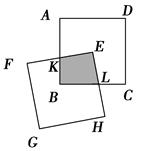
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的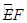 上时,
上时,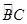 的长度等于( ).
的长度等于( ).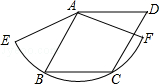
A.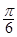 B.
B.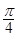 C.
C.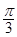 D.
D.
在矩形ABCD中,AB=1,AD= ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
A. |
B. |
C. |
D. |
设边长为3的正方形的对角线长为a,下列关于a的四种说法:① a是无理数;② a可以用数轴上的一个点来表示;③ 3<a<4;④ a是18的算术平方根。其中,所有正确说法的序号是
| A.①④ | B.②③ | C.①②④ | D.①③④ |
在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )
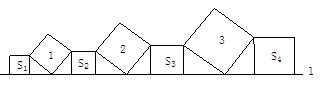
| A.6 | B.5 | C.4 | D.3 |
试题篮
()