初中数学圆内接四边形的性质选择题

如图，在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（4,0）∠AOC= 60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形OABC的两边分别交于点M,N（点M在点N的上方），若△OMN的面积为S，直线l的运动时间为t 秒（0≤t≤4）,则能大致反映S与t的函数关系的图象是（       ）

如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为(     )
A．90°     B．60°      C．45°      D．30°

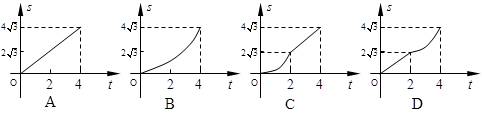
如图，从边长为（a＋4）cm的正方形纸片中剪去一个边长为cm的正方形，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积（    ）

A．	B．
C．	D．

已知四边形的对角线互相垂直，则顺次连接该四边形各边中点所得的四边形是       (      )

A．梯形

B．矩形

C．菱形

D．正方形

已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是

A．矩形

B．菱形

C．等腰梯形

D．正方形

四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有    
A．1组             B．2组             C．3组             D．4组

如图，在直角梯形中，AB∥CD；⊥动点从点出发，沿，运动至点停止．设点运动的路程为，的面积为，如果关于的函数图象如图所示，则的面积是（   ）

A．3

B．4

C．5

D．6

如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）.以BD、BF为邻边作平行四边形BDEF，又APBE（点P、E在直线AB的同侧），如果，那么△PBC的面积与△ABC面积之比为【   】

A.             B.              C.             D.

如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使得△AMN周长最小时，则∠AMN+∠ANM的度数为（    ）
A．100°        B．110°       C．120°       D．130°
              

如图 ，正方形ABCD的边长为4，M在DC上，且DM=1，N是AC上一动点，则DN+MN的最小值为（ ）．

A．3

B．4

C．5

D．

矩形具有而菱形不一定具有的性质是         (       )

A．对角线互相垂直

B．对角线相等

C．对角线互相平分

D．邻角互补

如图9四边形ABCD是菱形，且，是等边三角形，M为对角线BD(不含B点)上任意一点，将BM绕点B逆时针旋转得到BN，连接EN、AM、CM，则下列五个结论中正确的是（   ）

①若菱形ABCD的边长为1,则的最小值1;
②；
③；④连接AN，则；
⑤当的最小值为时，菱形ABCD的边长为2.

A．①②③

B．②④⑤

C．①②⑤

D．②③⑤

如图，正方形ABCE的边长为1，点M、N分别在BC、CD上，且△CMN的周长为2，则△MAN的面积的最小值为（  ）
A、       B、     C、    D、

如图，E、F、G、H分别是BD、BC、AC、AD的中点，且AB＝CD．下列结论：

①EG⊥FH，②四边形EFGH是矩形，③HF平分∠EHG，④EG＝(BC－AD)，⑤四边形
EFGH是菱形．其中正确的个数是【   】
A．1          B．2          C．3          D．4  

如图2，四边形ABCD中，E是BC的中点，连结DE并延长，交AB的延长线
于点F，AB=BF．添加一个条件，使四边形ABCD是平行四边形．下列条件中正确的是（   ）

A．AD=BC

B．CD=BF

C．∠F=∠CDE

D．∠A=∠C