初中数学圆内接四边形的性质计算题

已知, ∥，，试解答下列问题：
（1）如图所示，则___________°，并判断OB与AC平行吗？为什么？

（2）如图，若点在线段上，且满足 ，并且平分．则的度数等于_____________°；

（3）在第（2）题的条件下，若平行移动，如图．

①求:的值；
②当时，求的度数（直接写出答案，不必写出解答过程）．

如图所示，在长和宽分别是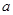、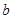的矩形纸片的四个角都剪去一个边长为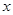的小正方形．

（1）用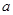、、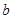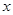表示纸片剩余部分的面积；
（2）当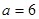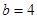，，且剪去部分的面积等于剩余部分的面积时，求正方形的边长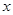的值．

在矩形中，，，点从点沿矩形的边以的速度经向运动，点从点出发沿矩形的边以的速度经向运动，点、同时运动，且一点到达终点另一点也停止运动，求几秒后以、、为顶点的三角形的面积等于6平方厘米？

如图，正方形ABCD的边长为3，E，F 分别是AB，BC边上的点，且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.

（1）求证：EF=FM；
（2）当AE=1时，求EF的长.

如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F，另一边交CB的延长线于点G.

（1）求证：EF＝EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变．（1）中的结论是否仍然成立？若成立，情给予证明；若不成立，请说明理由；

如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．

（1）求证：四边形DEGF是平行四边形；
（2）当点G是BC的中点时，求证：四边形DEGF是菱形．

如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，

（1）求的值为          .
（2）求证：AE=EP；
（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．

如图所示，已知BD⊥CD于D，EF⊥CD于F，，，其中为锐角，求证：。

如图，E是矩形ABCE的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H。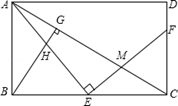

（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长。

两组邻边分别相等的四边形我们称它为筝形．
如图，在筝形中，，，，相交于点，

（1）求证：①；
②，；
（2）如果，，求筝形的面积．

已知：如图，为平行四边形ABCD的对角线，为的中点，于点，与，分别交于点．

求证：⑴．
⑵

如图所示，把长方形ABCD的纸片，沿EF线折叠后，ED与BC的交点为G，点D、C分别落在D^/、C^/的位置上，若∠1=70°，求∠2、∠EFG的度数.

如图，在菱形ABCD中，E是AB的中点，且DE⊥AB．

求∠ABD的度数
若菱形的边长为2，求菱形的面积

矩形的两条边长分别是和，求该矩形的面积和对角线的长.