(如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.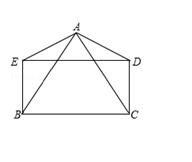
求证:四边形BCDE是矩形.
如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
如图,四边形ABCD、DEFG都是正方形,连接AE、CG、AE与CG相交于点M,CG与AD相交于点N.
求证:(1) ;
;
(2)
(1)知识再现
如图(1):若点A,B在直线l同侧,A,B到l的距离分别是3和2,AB=4,现在直线l上找一点P,使AP+BP的值最小,做法如下;
作点A关于直线l的对称点A′,连接BA′,与直线l的交代就是所求的点P,线段BA′的长度即为AP+BP的最小值,请你求出这个最小值.
(2)实践应用
①如图(2),⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是 ;
②如图(3),Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为 ;
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为 ;
③如图(4),菱形ABCD中AB=2,∠A=120°,点P,Q,K,分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 ;
④如图(5),在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD= ,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
(3)拓展延伸
如图(6),在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD,保留作图痕迹,不必写出作法.
(本小题满分10分)已知:如图,  ,
,  是□ABCD的对角线
是□ABCD的对角线 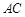 上的两点,
上的两点,  ,求证:
,求证:  .
.

如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径.
在矩形ABCD中,AB=6cm,BC=12cm,点P从点A 出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发以2cm/s的速度向点C移动.
(1)写出△DPQ的面积s与时间t的函数关系式.
(2)几秒钟后△DPQ的面积等于28cm2.
如图,矩形ABCD,E是AB上一点,且DE=AB,过C作CF⊥DE于F.
(1)猜想:AD与CF的大小关系;
(2)请证明上面的结论.
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.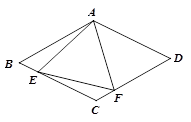
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,保留作图痕迹),并猜想BE与CD的关系:___________;你是通过证明_______________ 得到的。
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
试题篮
()