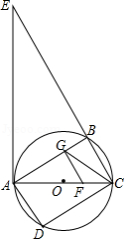
如图,四边形 内接于圆 , , 为直径,过点 作圆 的切线交 的延长线于点 ,过 的三等分点 (靠近点 作 的平行线交 于点 ,连接 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求 的长.
如图,已知四边形 内接于 , 是 的中点, 于 ,与 及 的延长线交于点 、 ,且 .
(1)求证: ;
(2)如果 , ,求 的值.

如图,四边形 内接于 , 是 的直径, 与 交于点 , 切 于点 .
(1)求证: ;
(2)若 , ,求证: .

如图,△ ABC内接于⊙ O, BC=2, AB= AC,点 D为 上的动点,且cos∠ ABC= .
(1)求 AB的长度;
(2)在点 D的运动过程中,弦 AD的延长线交 BC延长线于点 E,问 AD• AE的值是否变化?若不变,请求出 AD• AE的值;若变化,请说明理由;
(3)在点 D的运动过程中,过 A点作 AH⊥ BD,求证: BH= CD+ DH.

如图,四边形 内接于圆, ,对角线 平分 .
(1)求证: 是等边三角形;
(2)过点 作 交 的延长线于点 ,若 , ,求 的面积.

如图,已知 AD是△ ABC的外角∠ EAC的平分线,交 BC的延长线于点 D,延长 DA交△ ABC的外接圆于点 F,连接 FB, FC.
(1)求证:∠ FBC=∠ FCB;
(2)已知 FA• FD=12,若 AB是△ ABC外接圆的直径, FA=2,求 CD的长.

如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
(Ⅱ)若 ,AD=AP,求证:PD是⊙O的切线.

已知关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)当 时,方程的两根分别是矩形的长和宽,求该矩形外接圆的直径.
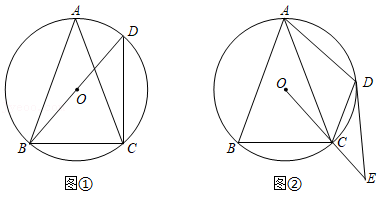
已知 内接于 , , ,点 是 上一点.
(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 ,连接 ,过点作 的切线,与 的延长线交于点 ,求 的大小.
如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)求证: ;
(2)若 , , ,求 的值.

如图,在以线段 为直径的 上取一点 ,连接 、 .将 沿 翻折后得到 .
(1)试说明点 在 上;
(2)在线段 的延长线上取一点 ,使 .求证: 为 的切线;
(3)在(2)的条件下,分别延长线段 、 相交于点 ,若 , ,求线段 的长.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

试题篮
()