如图,长方形纸片 中,AB=10,将纸片折叠,使顶点
中,AB=10,将纸片折叠,使顶点 落在边
落在边 上的
上的 点处,折痕的一端
点处,折痕的一端 点在边
点在边 上.
上.

图(2)
(1)如图(1),当折痕的另一端 在
在 边上且AE=5时,求AF的长
边上且AE=5时,求AF的长
(2)如图(2),当折痕的另一端 在
在 边上且BG=13时,求AF的长.
边上且BG=13时,求AF的长.
如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
(1)求△CPQ的面积S与时间t之间的函数关系式;
(2)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值.
(3)在P、Q移动的过程中,当△CPQ为等腰三角形时,直接写出t的值;
如图1是矩形纸片ABCD连续两次对折展开平铺后的图形,折痕分别为EF,MN,GH.
(1)如图2,连接BD,与折痕GH,EF,MN分别交于点S,O,T,求证:OE=OF;
(2)如图3,连接ET并延长CD交于点Q,连接FS并延长AB交于点P,连接EP,FQ.求证:四边形EPFQ是菱形;
(3)若四边形EPFQ是正方形,则矩形ABCD需满足的条件是______.
如图,在菱形ABCD中,对角线AC与BD相交于点O.CE∥BD,DE∥AC,连接OE.
求证:OE=AD.
如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.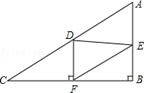
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△DEF是直角三角形时,求x的值.
如图,在正方形ABCD中,边长AB=3,点E(与B,C不重合)是BC边上任意一点,把EA绕点E顺时针方向旋转90°到EF,连接CF.
(1)求证:CF是正方形ABCD的外角平分线;
(2)当∠BAE=30°时,求CF的长.
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数 (x>0)的图象经过BC边上的中点D,交AB于点E.
(x>0)的图象经过BC边上的中点D,交AB于点E.
(1)k的值为_________;
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.
(1)作点P,使它与点O关于点E成中心对称,连接CP、DP;
(2)若四边形ABCD是矩形,试判断(1)中所得四边形CODP的形状并说明理由;
(3)若(1)中所得四边形CODP是正方形,请用图中的字母和符号表示四边形ABCD应满足的条件:_________.
如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:

(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,过C直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
试题篮
()