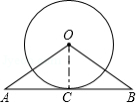
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
在屏幕上有如下内容:
如图,内接于
,直径
的长为2,过点
的切线交
的延长线于点
.张老师要求添加条件后,编制一道题目,并解答.
(1)在屏幕内容中添加条件,求
的长.请你解答.
(2)以下是小明、小聪的对话:
小明:我加的条件是,就可以求出
的长
小聪:你这样太简单了,我加的是,连结
,就可以证明
与
全等.
参考此对话,在屏幕内容中添加条件,编制一道题目(可以添线添字母),并解答.

如图,在 中, ,以点 为圆心、 的长为半径的 恰好经过 的中点 ,连接 , , , 与 交于点 .
(1)求证: 与 相切.
(2)若 ,求 的长.

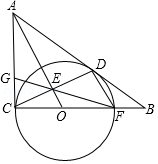
如图, 与 的直角边 和斜边 分别相切于点 、 ,与边 相交于点 , 与 相交于点 ,连接 并延长交 边于点 .
(1)求证: ;
(2)若 , ,求 的长.
已知是
的直径,弦
与
相交,
,
如图①,若
为
的中点,求
和
的大小;
(Ⅱ)如图②,过点作
的切线,与
的延长线交于点
,若
,求
的大小.

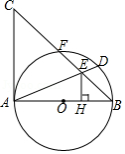
如图, 是 的直径, 是 的弦,直线 与 相切于点 ,过点 作 于点 .
(1)求证: ;
(2)若 , ,则 的半径是 .

如图,已知 为 直径, 是 的切线,连接 交 于点 ,取 的中点 ,连接 交 于点 ,过点 作 于 .
(1)求证: ;
(2)若 , ,求 和 的长.
如图,在 中, ,以 为直径的半圆 交 于点 ,过点 作半圆 的切线,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

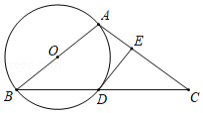
如图, 是 的直径,点 、 在 上,且 ,连接 、 ,过点 作 的切线,分别与 、 的延长线交于点 、 .
(1)求证: ;
(2)若 , ,求线段 的长.

如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
如图1,平行四边形 中, , , ,点 在边 上运动,以 为圆心, 为半径的 与对角线 交于 , 两点.
(1)如图2,当 与边 相切于点 时,求 的长;
(2)不难发现,当 与边 相切时, 与平行四边形 的边有三个公共点,随着 的变化, 与平行四边形 的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的 的值的取值范围 .

如图,已知 是 的直径, 是 延长线上一点, 切 于点 , 是 的弦, ,垂足为 .
(1)求证: .
(2)过点 作 交 于点 ,交 于点 ,连接 ,若 , ,求 的长.

如图, 是 的直径,点 在 的延长线上, 与 相切于点 , ,交 的延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.

试题篮
()