如图, 中, ,以点 为圆心, 为半径作 , 为 上一点,连接 、 , , 平分 .
(1)求证: 是 的切线;
(2)延长 、 相交于点 ,若 ,求 的值.
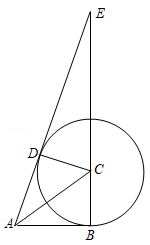
如图,在 中, , 的平分线交 于点 ,点 在 上,以点 为圆心, 为半径的圆恰好经过点 ,分别交 , 于点 , .
(1)试判断直线 与 的位置关系,并说明理由;
(2)若 , ,求阴影部分的面积(结果保留 .

已知:如图,在 中, ,点 是底边 上一点且满足 , 是 的外接圆,过点 作 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

如图,点 是 的内心, 的延长线交 于点 ,交 的外接圆 于点 ,连接 ,过点 作直线 ,使 .
(1)求证:直线 是 的切线;
(2)求证: .

如图,在 中, 是直径,弦 ,垂足为 , 为 上一点, 为弦 延长线上一点,连接 并延长交直径 的延长线于点 ,连接 交 于点 ,若 .
(1)求证: 是 的切线;
(2)若 的半径为8, ,求 的长.
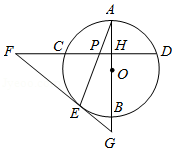
如图,在 中, ,点 是 边长一点, ,垂足为点 ,点 在线段 的延长线上,且 经过 , 两点.
(1)判断直线 与 的位置关系,并说明理由;
(2)若 的半径为2, 的长为 ,请求出 的度数.
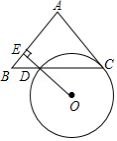
如图,在 中, ,以 为直径的 分别与 、 交于点 、 ,过点 作 于点 .
(1)若 的半径为3, ,求阴影部分的面积;
(2)求证: 是 的切线;
(3)求证: .

如图,在 中, ,以 为直径的 分别交线段 , 于点 , ,过点 作 ,垂足为 ,线段 , 的延长线相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.

如图,点 在以 为直径的 上, 的角平分线与 相交于点 ,与 相交于点 ,延长 至 ,连结 ,使得 ,过点 作 的平行线与 的延长线交于点 .
(1)求证: 与 相切;
(2)试给出 、 、 之间的数量关系,并予以证明.

如图,在 中, ,以 为直径的 交 于点 , 交 的延长线于点 ,交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,在 中, , 是 的平分线,以 为直径的 交 边于点 ,连接 ,过点 作 ,交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
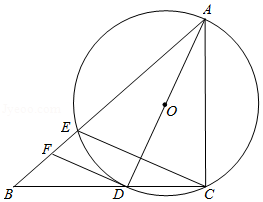
如图,点 在以 为直径的 上,点 是 的中点,连接 并延长交 于点 ,作 , 交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

如图,已知 是 外一点.用两种不同的方法过点 作 的一条切线.
要求:(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.

如图, 为 的直径, 为 上一点, 的平分线交 于点 , 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)过点 作 于点 ,若 , ,求图中阴影部分的面积.

试题篮
()