如图,长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°,则点A翻滚到A2位置时共走过的路径长为( )

| A.10cm | B. cm cm |
C. cm cm |
D. cm cm |
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则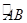 的长为( )
的长为( )

| A.π | B.6π | C.3π | D.1.5π |
如图,在 中, , ,以 的中点 为圆心 分别与 , 相切于 , 两点,则 的长为

A. B. C. D.
我们把1,1,2,3,5,8,13,21, 这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作 圆弧 , , , 得到斐波那契螺旋线,然后顺次连接 , , , 得到螺旋折线(如图),已知点 , , ,则该折线上的点 的坐标为
A. B. C. D.
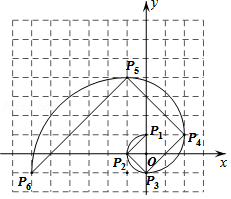
如图,放置在直线 上的扇形 .由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径 , ,则点 所经过的运动路径的长是
A. B. C. D.
如图,将矩形 绕其右下角的顶点按顺时针方向旋转 至图①位置,继续绕右下角的顶点按顺时针方向旋转 至图②位置,以此类推,这样连续旋转2017次.若 , ,则顶点 在整个旋转过程中所经过的路径总长为

A. B. C. D.
把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是

A. B. C. D.
如图, 为 的直径, , 弦 ,垂足为 , 切 于点 , ,连接 、 、 ,下列结论不正确的是

| A. |
|
B. |
是等边三角形 |
| C. |
|
D. |
的长为 |
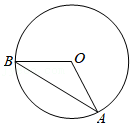
如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()