如图,点 C为△ ABD的外接圆上的一动点(点 C不在 上,且不与点 B, D重合),∠ ACB=∠ ABD=45°
(1)求证: BD是该外接圆的直径;
(2)连结 CD,求证: ;
(3)若△ ABC关于直线 AB的对称图形为△ ABM,连接 DM,试探究 DM 2, AM 2, BM 2三者之间满足的等量关系,并证明你的结论.

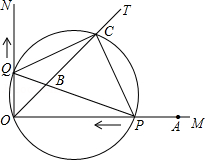
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
(1)如图1,点为矩形
对角线
上一点,过点
作
,分别交
、
于点
、
.若
,
,
的面积为
,
的面积为
,则
;
(2)如图2,点为
内一点(点
不在
上),点
、
、
、
分别为各边的中点.设四边形
的面积为
,四边形
的面积为
(其中
,求
的面积(用含
、
的代数式表示);
(3)如图3,点为
内一点(点
不在
上),过点
作
,
,与各边分别相交于点
、
、
、
.设四边形
的面积为
,四边形
的面积为
(其中
,求
的面积(用含
、
的代数式表示);
(4)如图4,点、
、
、
把
四等分.请你在圆内选一点
(点
不在
、
上),设
、
、
围成的封闭图形的面积为
,
、
、
围成的封闭图形的面积为
,
的面积为
,
的面积为
,根据你选的点
的位置,直接写出一个含有
、
、
、
的等式(写出一种情况即可).

如图,半径为4的中,弦
的长度为
,点
是劣弧
上的一个动点,点
是弦
的中点,点
是弦
的中点,连接
、
、
.
(1)求的度数;
(2)当点沿着劣弧
从点
开始,逆时针运动到点
时,求
的外心
所经过的路径的长度;
(3)分别记,
的面积为
,
,当
时,求弦
的长度.

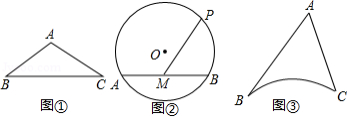
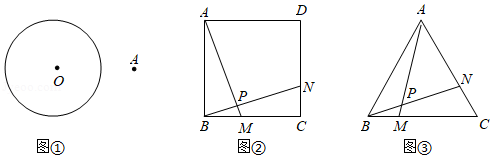
(1)方法选择
如图①,四边形是
的内接四边形,连接
,
,
.求证:
.
小颖认为可用截长法证明:在上截取
,连接
小军认为可用补短法证明:延长至点
,使得
请你选择一种方法证明.
(2)类比探究
[探究1]
如图②,四边形是
的内接四边形,连接
,
,
是
的直径,
.试用等式表示线段
,
,
之间的数量关系,并证明你的结论.
[探究2]
如图③,四边形是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式是
.
(3)拓展猜想
如图④,四边形是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式是 .

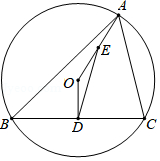
如图,已知锐角三角形内接于圆
,
于点
,连接
.
(1)若,
①求证:.
②当时,求
面积的最大值.
(2)点在线段
上,
,连接
,设
,
,
是正数),若
,求证:
.
已知的直径
,弦
与弦
交于点
.且
,垂足为点
.

(1)如图1,如果,求弦
的长;
(2)如图2,如果为弦
的中点,求
的余切值;
(3)联结、
、
,如果
是
的内接正
边形的一边,
是
的内接正
边形的一边,求
的面积.
如图,已知的半径长为1,
、
是
的两条弦,且
,
的延长线交
于点
,联结
、
.
(1)求证:;
(2)当是直角三角形时,求
、
两点的距离;
(3)记、
、
的面积分别为
、
、
,如果
是
和
的比例中项,求
的长.

问题提出
(1)如图①,在中,
,
,则
的外接圆半径
的值为 .
问题探究
(2)如图②,的半径为13,弦
,
是
的中点,
是
上一动点,求
的最大值.
问题解决
(3)如图③所示,、
、
是某新区的三条规划路,其中
,
,
,
所对的圆心角为
,新区管委会想在
路边建物资总站点
,在
,
路边分别建物资分站点
、
,也就是,分别在
、线段
和
上选取点
、
、
.由于总站工作人员每天都要将物资在各物资站点间按
的路径进行运输,因此,要在各物资站点之间规划道路
、
和
.为了快捷、环保和节约成本.要使得线段
、
、
之和最短,试求
的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
问题提出
(1)如图①,在中,
,
,点
关于
所在直线的对称点为
,则
的长度为 .
问题探究
(2)如图②,半圆的直径
,
是
的中点,点
在
上,且
,
是
上的动点,试求
的最小值.
问题解决
(3)如图③,扇形花坛的半径为
,
.根据工程需要.现想在
上选点
,在边
上选点
,在边
上选点
,用装饰灯带在花坛内的地面上围成一个
,使晚上点亮时,花坛中的花卉依然赏心悦目.为了既节省材料,又美观大方,需使得灯带
的长度最短,并且用长度最短的灯带围成的
为等腰三角形.试求
的值最小时的等腰
的面积.(安装损耗忽略不计)

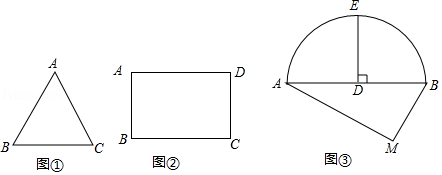
问题提出
(1)如图①,是等边三角形,
,若点
是
的内心,则
的长为 ;
问题探究
(2)如图②,在矩形中,
,
,如果点
是
边上一点,且
,那么
边上是否存在一点
,使得线段
将矩形
的面积平分?若存在,求出
的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由草地和弦
与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在
处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于
(即每次喷灌时喷灌龙头由
转到
,然后再转回,这样往复喷灌.
同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出,
,
的面积为
;过弦
的中点
作
交
于点
,又测得
.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
(1)如图①,点是
外一点,点
是
上一动点.若
的半径为3,且
,则点
到点
的最短距离为 ;
(2)如图②,已知正方形的边长为4,点
、
分别从点
、
同时出发,以相同的速度沿边
、
方向向终点
和
运动,连接
和
交于点
,则点
到点
的最短距离为 ;
(3)如图③,在等边中,
,点
、
分别从点
、
同时出发,以相同的速度沿边
、
方向向终点
和
运动,连接
和
交于点
,求
面积的最大值,并说明理由.
在中,
,
分别是
两边的中点,如果
上的所有点都在
的内部或边上,则称
为
的中内弧.例如,图1中
是
的一条中内弧.

(1)如图2,在中,
,
,
分别是
,
的中点,画出
的最长的中内弧
,并直接写出此时
的长;
(2)在平面直角坐标系中,已知点,
,
,
,在
中,
,
分别是
,
的中点.
①若,求
的中内弧
所在圆的圆心
的纵坐标的取值范围;
②若在中存在一条中内弧
,使得
所在圆的圆心
在
的内部或边上,直接写出
的取值范围.
对于平面直角坐标系中的图形
,
,给出如下定义:
为图形
上任意一点,
为图形
上任意一点,如果
,
两点间的距离有最小值,那么称这个最小值为图形
,
间的“闭距离“,记作
.
已知点,
,
.
(1)求(点
,
;
(2)记函数的图象为图形
.若
,直接写出
的取值范围;
(3)的圆心为
,半径为1.若
,直接写出
的取值范围.
试题篮
()