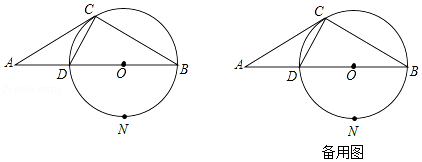
如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

问题提出
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.

阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
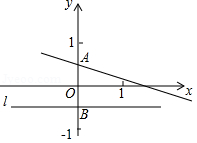
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在 上运动, 的半径为1,圆心 在过点 且与 轴垂直的直线上.对于 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.

如图①,在平面直角坐标系中,圆心为 的动圆经过点 且与 轴相切于点 .
(1)当 时,求 的半径;
(2)求 关于 的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当 的半径为1时,若 与以上(2)中所得函数图象相交于点 、 ,其中交点 在点 的右侧,请利用图②,求 的大小.

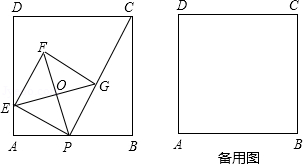
如图,已知正方形 的边长为4,点 是 边上的一个动点,连接 ,过点 作 的垂线交 于点 ,以 为边作正方形 ,顶点 在线段 上,对角线 、 相交于点 .
(1)若 ,则 ;
(2)①求证:点 一定在 的外接圆上;
②当点 从点 运动到点 时,点 也随之运动,求点 经过的路径长;
(3)在点 从点 到点 的运动过程中, 的外接圆的圆心也随之运动,求该圆心到 边的距离的最大值.
如图1是一个用铁丝围成的篮筐,我们来仿制一个类似的柱体形篮筐.如图2,它是由一个半径为 、圆心角 的扇形 ,矩形 、 ,及若干个缺一边的矩形状框 、 、 、 , 围成,其中 、 、 在 上, 、 、 与 、 、 分别在半径 和 上, 、 、 、 和 、 分别在 和 上, 于 , 于 , , 、 、 、 依次等距离平行排放(最后一个矩形状框的边 与点 间的距离应不超过 ,
(1)求 的值;
(2)问: 与点 间的距离能否等于 ?如果能,求出这样的 的值,如果不能,那么它们之间的距离是多少?

问题背景:
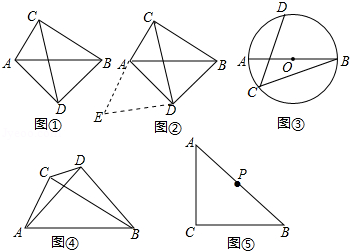
如图①,在四边形 中, , ,探究线段 , , 之间的数量关系.
小吴同学探究此问题的思路是:将 绕点 ,逆时针旋转 到 处,点 , 分别落在点 , 处(如图② ,易证点 , , 在同一条直线上,并且 是等腰直角三角形,所以 ,从而得出结论: .
简单应用:
(1)在图①中,若 , ,则 .
(2)如图③, 是 的直径,点 、 在 上, ,若 , ,求 的长.
拓展规律:
(3)如图④, , ,若 , ,求 的长(用含 , 的代数式表示)
(4)如图⑤, , ,点 为 的中点,若点 满足 , ,点 为 的中点,则线段 与 的数量关系是 .
如图,正方形 的边长为1,点 在射线 上(异于点 、 ,直线 与对角线 及射线 分别交于点 、
(1)若 ,求 的度数;
(2)若点 在线段 上,过点 作 ,垂足为 ,当 时,求 的长;
(3)以 为直径作 .
①判断 和 的位置关系,并说明理由;
②当直线 与 相切时,直接写出 的长.
如图,动点 在以 为圆心, 为直径的半圆弧上运动(点 不与点 、 及 的中点 重合),连接 .过点 作 于点 ,以 为边在半圆同侧作正方形 ,过点 作 的切线交射线 于点 ,连接 、 .
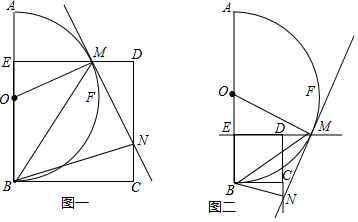
(1)探究:如图一,当动点 在 上运动时;
①判断 是否成立?请说明理由;
②设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
③设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点 在 上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
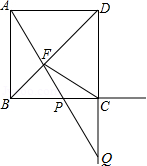
已知在平面直角坐标系中,点 A(3,0), B(﹣3,0), C(﹣3,8),以线段 BC为直径作圆,圆心为 E,直线 AC交⊙ E于点 D,连接 OD.
(1)求证:直线 OD是⊙ E的切线;
(2)点 F为 x轴上任意一动点,连接 CF交⊙ E于点 G,连接 BG;
①当tan∠ ACF= 时,求所有 F点的坐标 (直接写出);
②求 的最大值.

在平面直角坐标系中,已知点 A(﹣2,0), B(2,0), C(3,5).
(1)求过点 A, C的直线解析式和过点 A, B, C的抛物线的解析式;
(2)求过点 A, B及抛物线的顶点 D的⊙ P的圆心 P的坐标;
(3)在抛物线上是否存在点 Q,使 AQ与⊙ P相切,若存在请求出 Q点坐标.

试题篮
()