初中数学作图—基本作图试题

如图，已知线段 ，分别以 、 为圆心，大于 $\frac{1}{2}$ AB为半径作弧，连接弧的交点得到直线 ，在直线 上取一点 ，使得 ，延长 至 ，求 的度数为 　　

A．

B．

C．

D．

如图，AE∥BF，AC平分∠BAE，交BF于C．

（1）尺规作图：过点B作AC的垂线，交AC于O，交AE于D，（保留作图痕迹，不写作法）；

（2）在（1）的图形中，找出两条相等的线段，并予以证明．

如图，在 中， ， ， ．

（1）利用尺规作线段 的垂直平分线 ，垂足为 ，交 于点 ，（保留作图痕迹，不写作法）

（2）若 的周长为 ，先化简 ，再求 的值．

如图，已知△ ABC中， D为 AB的中点．

（1）请用尺规作图法作边 AC的中点 E，并连接 DE（保留作图痕迹，不要求写作法）；

（2）在（1）的条件下，若 DE＝4，求 BC的长．

如图，在▱ ABCD中， AB＝3， BC＝5，以点 B的圆心，以任意长为半径作弧，分别交 BA、 BC于点 P、 Q，再分别以 P、 Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠ ABC内交于点 M，连接 BM并延长交 AD于点 E，则 DE的长为 　　．

如图，利用尺规，在△ ABC的边 AC上方作∠ CAE＝∠ ACB，在射线 AE上截取 AD＝ BC，连接 CD，并证明： CD∥ AB（尺规作图要求保留作图痕迹，不写作法）

根据圆规作图的痕迹，可用直尺成功地找到三角形内心的是 $($ 　　 $)$

A．		B．
C．		D．

在四边形 $\mathit{ABCD}$ 中， $\mathit{AD}//\mathit{BC}$ ， $\angle D=90°$ ， $\mathit{AD}=8$ ， $\mathit{BC}=6$ ，分别以 $A$ ， $C$ 为圆心，大于 $\frac{1}{2}\mathit{AC}$ 的长为半径作弧，两弧交于点 $E$ ，作射线 $\mathit{BE}$ 交 $\mathit{AD}$ 于点 $F$ ，交 $\mathit{AC}$ 于点 $O$ ，若点 $O$ 是 $\mathit{AC}$ 的中点，则 $\mathit{CD}$ 的长为 $($ 　　 $)$

A．

$4\sqrt{2}$

B．

$2\sqrt{10}$

C．

6

D．

8

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=5$， $\mathit{AC}=8$， $\mathit{BC}=9$，以 $A$为圆心，以适当的长为半径作弧，交 $\mathit{AB}$于点 $M$，交 $\mathit{AC}$于点 $N$．分别以 $M$， $N$为圆心，以大于 $\frac{1}{2}\mathit{MN}$的长为半径作弧，两弧在 $\angle \mathit{BAC}$的内部相交于点 $G$，作射线 $\mathit{AG}$，交 $\mathit{BC}$于点 $D$，点 $F$在 $\mathit{AC}$边上， $\mathit{AF}=\mathit{AB}$，连接 $\mathit{DF}$，则 $\mathit{\Delta CDF}$的周长为　　．

如图，菱形 $\mathit{ABCD}$ 的边长为4， $\angle A=45°$ ，分别以点 $A$ 和点 $B$ 为圆心，大于 $\frac{1}{2}\mathit{AB}$ 的长为半径作弧，两弧相交于 $M$ ， $N$ 两点，直线 $\mathit{MN}$ 交 $\mathit{AD}$ 于点 $E$ ，连接 $\mathit{CE}$ ，则 $\mathit{CE}$ 的长为 　 　．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ， $\mathit{AC}=2\mathit{BC}$ ，分别以点 $A$ 和 $B$ 为圆心，以大于 $\frac{1}{2}\mathit{AB}$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ，作直线 $\mathit{MN}$ ，交 $\mathit{AC}$ 于点 $E$ ，连接 $\mathit{BE}$ ，若 $\mathit{CE}=3$ ，则 $\mathit{BE}$ 的长为 　　．

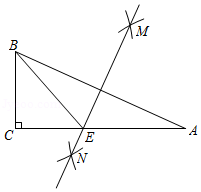
如图，在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{BAC}=90°$ ， $\mathit{AB}>\mathit{AC}$ ．按下列步骤作图：

①分别以点 $B$ 和点 $C$ 为圆心，大于 $\mathit{BC}$ 一半的长为半径作圆弧，两弧相交于点 $M$ 和点 $N$ ；

②作直线 $\mathit{MN}$ ，与边 $\mathit{AB}$ 相交于点 $D$ ，连结 $\mathit{CD}$ ．

下列说法不一定正确的是 $($ 　　 $)$

A．

$\angle \mathit{BDN}=\angle \mathit{CDN}$

B．

$\angle \mathit{ADC}=2\angle B$

C．

$\angle \mathit{ACD}=\angle \mathit{DCB}$

D．

$2\angle B+\angle \mathit{ACD}=90°$

如图，在 $\mathit{\Delta ABC}$ 中，按以下步骤作图：

①以点 $B$ 为圆心，任意长为半径作弧，分别交 $\mathit{AB}$ 、 $\mathit{BC}$ 于点 $D$ 、 $E$ ．

②分别以点 $D$ 、 $E$ 为圆心，大于 $\frac{1}{2}\mathit{DE}$ 的同样长为半径作弧，两弧交于点 $F$ ．

③作射线 $\mathit{BF}$ 交 $\mathit{AC}$ 于点 $G$ ．

如果 $\mathit{AB}=8$ ， $\mathit{BC}=12$ ， $\mathit{\Delta ABG}$ 的面积为18，则 $\mathit{\Delta CBG}$ 的面积为 　 　．

人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：

已知：．

求作：的平分线．

作法：（1）以点为圆心，适当长为半径画弧，交于点，交于点．

（2）分别以点，为圆心，大于的长为半径画弧，两弧在的内部相交于点．

（3）画射线，射线即为所求（如图）．

请你根据提供的材料完成下面问题．

（1）这种作已知角的平分线的方法的依据是　　．（填序号）

①②③④

（2）请你证明为的平分线．

已知 $\angle \mathit{AOB}$ ，作 $\angle \mathit{AOB}$ 的平分线 $\mathit{OM}$ ，在射线 $\mathit{OM}$ 上截取线段 $\mathit{OC}$ ，分别以 $O$ 、 $C$ 为圆心，大于 $\frac{1}{2}\mathit{OC}$ 的长为半径画弧，两弧相交于 $E$ ， $F$ ．画直线 $\mathit{EF}$ ，分别交 $\mathit{OA}$ 于 $D$ ，交 $\mathit{OB}$ 于 $G$ ．那么 $\mathit{\Delta ODG}$ 一定是 $($ 　　 $)$

A．

锐角三角形

B．

钝角三角形

C．

等腰三角形

D．

直角三角形