如图,在四边形ABCD中, ,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若 , ,则BD= (提示:可连接BE)

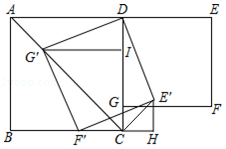
如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A. B. C. D.
一副三角板如图放置,将三角板 ADE绕点 A逆时针旋转α(0°<α<90°),使得三角板 ADE的一边所在的直线与 BC垂直,则α的度数为 .

(1)【探究发现】
如图1,∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处,∠ EOF=90°,将∠ EOF绕点 O旋转,旋转过程中,∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F(点 F与点 C, D不重合).则 CE, CF, BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的"正方形 ABCD"改为"∠ BCD=120°的菱形 ABCD",其他条件不变,当∠ EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3,∠ BOD=120°, OD= , OB=4, OA平分∠ BOD, AB= ,且 OB>2 OA,点 C是 OB上一点,∠ CAD=60°,求 OC的长.

如图,在△ ABC中,∠ CAB=55°,∠ ABC=25°,在同一平面内,将△ ABC绕 A点逆时针旋转70°得到△ ADE,连接 EC,则tan∠ DEC的值是 .

如图,在Rt△ ACB中,∠ ACB=90°, AC= BC, D是 AB上的一个动点(不与点 A, B重合),连接 CD,将 CD绕点 C顺时针旋转90°得到 CE,连接 DE, DE与 AC相交于点 F,连接 AE.下列结论:
①△ ACE≌△ BCD;
②若∠ BCD=25°,则∠ AED=65°;
③ DE 2=2 CF• CA;
④若 AB=3 , AD=2 BD,则 AF= .
其中正确的结论是 .(填写所有正确结论的序号)

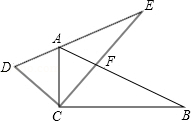
两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF= cm.
如图所示,正方形ABCD对角线AC所在直线上有一点O,OA=AC=2,将正方形绕O点顺时针旋转60°,在旋转过程中,正方形扫过的面积是 .

如图是一副三角尺 ABC和与 DEF拼成的图案,若将三角尺 DEF绕点 M按顺时针方向旋转,则边 DE与边 AB第一次平行时,旋转角的度数是( )

| A. |
75° |
B. |
60° |
C. |
45° |
D. |
30° |
如图,在矩形 ABCD中, AB=3, BC=4,将矩形 ABCD绕点 C按顺时针方向旋转α角,得到矩形 A' B' C' D', B' C与 AD交于点 E, AD的延长线与 A' D'交于点 F.

(1)如图①,当α=60°时,连接 DD',求 DD'和 A' F的长;
(2)如图②,当矩形 A' B' CD'的顶点 A'落在 CD的延长线上时,求 EF的长;
(3)如图③,当 AE= EF时,连接 AC, CF,求 AC• CF的值.
如图,Rt△ ABC中,∠ ACB=90°,在以 AB的中点 O为坐标原点, AB所在直线为 x轴建立的平面直角坐标系中,将△ ABC绕点 B顺时针旋转,使点 A旋转至 y轴的正半轴上的 A′处,若 AO= OB=1,则阴影部分面积为( )

| A. |
π |
B. |
π﹣1 |
C. |
+1 |
D. |
|
如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=1,则阴影部分面积为( )

A. πB. π﹣1C. +1D.
如图,在Rt△ ABC中,∠ C=90°, AC=3, BC=4,把△ ABC绕 AB边上的点 D顺时针旋转90°得到△ A′ B′ C′, A′ C′交 AB于点 E,若 AD= BE,则△ A′ DE的面积是 .

如图,在Rt△ ABC中,∠ C=90°, M为 AB边的中点,将Rt△ ABC绕点 M旋转,使点 C与点 A重合得△ DEA, AE交 CB于点 N.若 AB=2 , AC=4,则 CN的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()