初中数学平行线分线段成比例试题

如果反比例函数过A（2，-3），则m=       。

反比例函数的图象在第一、三象限，则的取值范围是        ；在每一象限内y随x的增大而       。

已知反比例函数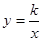图象过第二象限内的点A（-2，m）AB⊥x轴于B， Rt△AOB面积为3, 若直线y=ax+b经过点A，并且经过反比例函数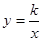的图象上另一点C（n，—），

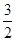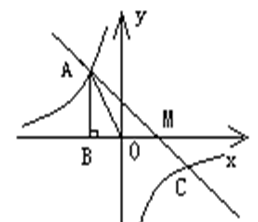
（1）反比例函数的解析式为          ，m=       ，n=         ；
（2）求直线y=ax+b的解析式；
（3）在y轴上是否存在一点P，使△PAO为等腰三角形，若存在，请直接写出P点坐标，若不存在，说明理由。

已知：与成正比例，且时，。
（1）试求与之间的函数关系式；
（2）当时，求的值；
（3）当取何值时， ？；

在反比例函数y＝的图像上有三点A₁（x₁,y₁）、A₂(x₂,y₂)、A₃(x₃,y₃)，已知x₁ < x₂ <0<x₃则下列各式中，正确的是（    ）
A 、y₁ <y₂<y₃        B、 y₃< y₂< y₁     C_、y₂< y₁< y₃      D、 y₃< y₁< y₂

直线y＝－2x－4与x轴交于点A，与y轴交于点B，将线段AB绕着平面内的某个点旋转180°后，得到点C、D，恰好落在反比例函数y＝的图象上，且D、C两点横坐标之比为3∶1，则k＝  ．

已知反比例函数的图象经过点P（1，－2），则这个函数的图象位于（）

A．第一、三象限

B．第二、三象限

C．第二、四象限

D．第三、四象限

如图，在平面直角坐标系中，反比例函数的图象与一次函数的图象的一个交点为.

（1）求反比例函数的解析式；
（2）设一次函数的图象与轴交于点，若是轴上一点，且满足的面积是3，直接写出点的坐标．

如图 ，反比例函数和上分别有两点B、C，且BC∥轴，点P是轴上一动点，则△BCP的面积是（    ）

A．5       B．5.5     C．6.5         D．10

已知水池的容量一定，当每小时的灌水量为q=3米³时，灌满水池所需的时间为t=12小时．
⑴写出灌水量q与灌满水池所需的时间t的函数关系式；
⑵求当灌满水池所需8小时时，每小时的灌水量．

函数y＝的图象与函数y＝x的图象没有交点，那么k的取值范围是        

若反比例函数y＝（k为常数，且k≠0）的图象过点（3，－4），则下列各点在该图象上的是

A．（6，－8）

B．(－6，8)

C．（－3，4）

D．(－3，－4)

如图，M为双曲线上的一点，过点M作x轴、y轴的垂线，分别交直线y＝－x＋m于点D、C两点，若直线y＝－x＋m与y轴交于点A，与x轴相交于点B，则AD•BC的值为      ．

已知反比例函数，下列结论不正确的是

A．图象必经过点(-1,2)	B．图象在第二、四象限内
C．y随x的增大而增大	D．若x＞1，则y＞-2

已知反比例函数,当m_______时,其图象的两个分支在第二､四象限内;当m_______时,其图象在每个象限内y随x的增大而减小