初中数学平行线分线段成比例试题

如图，已知A(-4,n)，B(1,-4)是一次函数的图象和反比例函数的图象的两个交点．

(1)求反比例函数和一次函数的解析式；
(2)求直线与轴的交点的坐标及△的面积；
(3)求不等式的解集（请直接写出答案）.

如图，一次函数的图象与反比例函数（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0），A点的横坐标为-1.

（1）求一次函数的解析式；
（2）设函数（x＞0）的图象与（x＜0）的图象关于y轴对称，在（x＞0）的图象上取一点P（P点的横坐标大于2），过P点作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．

如图，在平面直角坐标系中，函数的图象与一次函数的图象的交点为．

（1）求一次函数的解析式；
（2）设一次函数的图象与轴交于点，若是轴上一点，且满足的面积是4，求点的坐标．

已知反比例函数的图象过点M（－1，2），则此反比例函数的表达式为

A．y=

B．y=－

C．y=

D．y=－

已知反比例函数的图象经过点，则此反比例函数的图象在（    ）

A．第一、二象限	B．第一、三象限
C．第二、四象限	D．第三、四象限

某反比例函数的图象经过点(-2，3)，则此函数图象也经过点（ ）

A．(2，-3)

B．(-3，-3)

C．（2，3）

D．（-4，6）

如图，反比例函数y=（k＞0）与矩形OABC在第一象限相交于D、E两点，OA=2，OC=4，连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .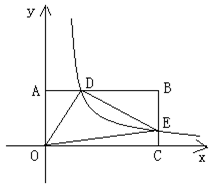

（1）①点B的坐标为       ；②S     S（填“＞”、“＜”、“=”）；
（2）当点D为线段AB的中点时，求k的值及点E的坐标；
（3）当S+S=2时，试判断△ODE的形状，并求△ODE的面积.

反比例函数的图象与一次函数y=ax+b的图象交于A（1，3）和B（n,-1）两点.

（1）求这两个函数的解析式，并画出草图;
（2）根据图象回答当x取何值时，反比例函数的值大于一次函数的值;
（3）连接OA、OB, 求⊿AOB的面积.

你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度是面条的粗细（横截面积）的反比例函数，其图像如图所示.


（1）写出与的函数关系式；
（2）若面条的总长度是50m时，面条的粗细是多少？
（3）当面条的粗细应不小于，面条的总长度最长是多少？

如图,△OPQ是边长为2的等边三角形,若反比例函数的图象过点P,则它的解析式是                 。

面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是                                                            （ 　　 ）

如图, 在函数(x>0)的图象上, 四边形COAB是正方形, 四边形FOEP是长方形, 点B、P在双曲线上,下列说法不正确的是                 (       )

A. 长方形BCFG和长方形GAEP的面积相等   
B. 点B的坐标是(4, 4)
C. 图象关于过OB的直线对称                 
D. 长方形FOEP与正方形COAB的面积相等

反比例函数的图象经过点（，3），则它还经过点  （     ）

A．（，-3）

B．（，）

C．（3，2）

D．（6，）

如图，在函数(x＜0)和(x＞0)的图象上，分别有A、B两点，若AB∥x轴且OA⊥OB，则A点坐标为     ．

已知关于x的函数y=k(x-1)和，它们在同一坐标系内大致图象是图中的