(本题6分)如图,已知直线 经过点P(
经过点P( ,
, ),点P关于
),点P关于 轴的对称点P′在反比例函数
轴的对称点P′在反比例函数 (
( )的图象上.
)的图象上.
(1)求 的值;
的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
某乡要在生活垃圾存放区建一个老年活动中心,这样必须把1 200 m3的生活垃圾运走.
(1)假如每天能运x m3,所需时间为y天,写出y与x之间的函数关系式;
(2)若每辆拖拉机一天能运12 m3,则5辆这样的拖拉机要多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
(本小题满分10分)如图,已知反比例函数 (
(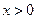 )的图象与一次函数
)的图象与一次函数 的图象交于
的图象交于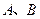 两点,点
两点,点 的坐标为
的坐标为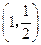 ,连接
,连接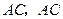 平行于
平行于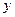 轴.
轴.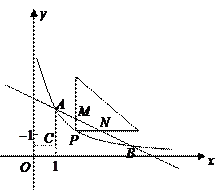
(1)求反比例函数的解析式及点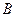 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点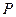 在反比例函数图象上的
在反比例函数图象上的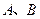 之间的部分滑动(不与
之间的部分滑动(不与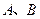 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于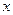 轴、
轴、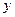 轴,且与线段
轴,且与线段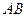 交于
交于 两点,试判断
两点,试判断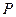 点在滑动过程中
点在滑动过程中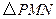 是否与
是否与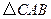 总相似,简要说明判断理由.
总相似,简要说明判断理由.
如图,点A,D在反比例函数y= (x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
(x>0)的图象上,点A的坐标是(2,4),接AD,过点A作AB⊥AD,交y轴于点B,过点D作DC⊥AD,交x轴于点C,连接BC,四边形ABCD为正方形.
(1)求点C的坐标;
(2)求点D的坐标.
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
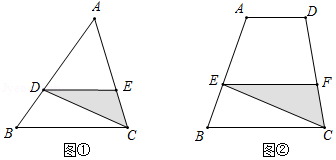
问题1:如图①,在 中, , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 的面积为 , 的面积为 .
(1)当 时, ;
(2)设 ,请你用含字母 的代数式表示 .
问题2:如图②,在四边形 中, , , , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 ,四边形 的面积为 , 的面积为 .请你利用问题1的解法或结论,用含字母 的代数式表示 .
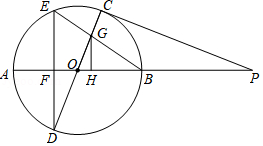
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
如图,在 中, ,点 从点 向点 运动,点 从点 沿射线 方向运动,且 ,连接 交 于 .
(1)如图1,当 时,求证: ;
(2)如图2,当 时,① , ,则 ;
②过点 作 于点 ,探究线段 , , 之间的数量关系,直接写出结论,不需证明.

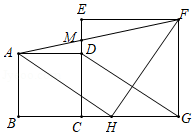
如图,正方形的边
在正方形
的边
上,连接
,过点
作
,交
于点
.连接
,
,其中
交
于点
.
(1)求证:为等腰直角三角形.
(2)若,
,求
的长.
已知一次函数 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数  (k为常数,
(k为常数, )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点 的坐标;
的坐标;
(2)观察图象,写出使函数值 的自变量
的自变量 的取值范围;
的取值范围;
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(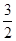 ,-2),反比例函数y=
,-2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.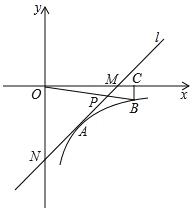
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y= 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC= .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
(8分)如图,四边形 是平行四边形,点
是平行四边形,点 .反比例函数
.反比例函数 的图象经过点
的图象经过点 ,点
,点 是一次函数
是一次函数 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数 的图象一定过点
的图象一定过点 ;
;
(3)对于一次函数 ,当
,当 的增大而增大时,确定点
的增大而增大时,确定点 横坐标的取值范围(不写过程,直接写出结果).
横坐标的取值范围(不写过程,直接写出结果).
在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
试题篮
()