已知:如图,直线 与反比例函数图象
与反比例函数图象 分别交于点
分别交于点 和点
和点 两点,与
两点,与 轴交于点
轴交于点 ,且以
,且以 为顶点的三角形面积为
为顶点的三角形面积为 ,点
,点 横坐标为
横坐标为 .
.
(1)则 = ;
= ;
(2)当 =1时,求
=1时,求 的值;
的值;
(3)求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围.
的取值范围.
如图,点 是反比例函数
是反比例函数 (x>0)的图象上一点,
(x>0)的图象上一点,
 轴正半轴于
轴正半轴于 ,
, 是
是 的中点;一次函数
的中点;一次函数 的图象过
的图象过 、
、 两点,并交于
两点,并交于 轴于
轴于 .
.
(1)直接写出点 、
、 的坐标;
的坐标;
(2)求一次函数和反比例函数的解析式;
(3)观察图象,请指出在 轴的右侧,当
轴的右侧,当 时
时 的取值范围.
的取值范围.
如图,是反比例函数 和
和 (k1>k2)在第一象限的图象,直线
(k1>k2)在第一象限的图象,直线
 ∥
∥ 轴,并分别交两条曲线于
轴,并分别交两条曲线于 、
、 两点。
两点。
(1)若点 的纵坐标是
的纵坐标是 ,则可得点
,则可得点 的纵坐标是 .
的纵坐标是 .
(2)若 ,则
,则 与
与 之间的关系是 .
之间的关系是 .
如图,已知直线 与双曲线
与双曲线 交于A(
交于A( ),B(
),B( )两点两点(A与B不重合),直线AB与x轴交于P(
)两点两点(A与B不重合),直线AB与x轴交于P( ,0),与y轴交于点C.
,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若 ,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示 之间的关系(不要求证明).
之间的关系(不要求证明).
如图,已知直线y=ax+b与双曲线 交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.
交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于点P(x0,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2).求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标;
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
我们知道,函数 的图像是由二次函数 的图像向右平移 个单位,再向上平移 个单位得到.类似地,函数 的图像是由反比例函数 理解应用像可以由函数 的图像向右平移个单位,再
函数
的图向上平移个单位得到,其对称中心坐标为.
灵活运用
如图,在平面直角坐标系xOy中,请根据所给的
的图像画出函数
的图像,并根据该图像指出,当
在什么范围内变化时,
?
实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为
;若在
(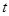 ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
.如果记忆存留量为
时是复习的"最佳时机点",且他第一次复习是在"最佳时机点"进行的,那么当x为何值时,是他第二次复习的"最佳时机点"?
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
.如果记忆存留量为
时是复习的"最佳时机点",且他第一次复习是在"最佳时机点"进行的,那么当x为何值时,是他第二次复习的"最佳时机点"?
张先生以按揭方式(首付一部分,剩余部分按每月分期付款)购买了价格为16万元的汽车,交了首付款之后每月还款y元,x个月结清,y与x之间的函数关系如图所示,根据图象提供的信息解答下列问题.
(1)确定y与x之间的函数关系式,并求出首付款的金额.
(2)张先生若打算120个月结清余款,每月应付多少元?
(3)若打算每月付款不超过1500元,问:张先生至少几个月才能结清余款?
某开发商准备开发建设一幢住宅区,工程需填土104米3,某工程队承包了该项填土任务.
(1)该工程队平均的填土量V(米3/天)与完成任务所需时间t(天)之间具有怎样的函数关系?
(2)该工程队共有10辆运输车,每辆车每天运土100米3,若工程必须在20天内完成任务,问:工程队每天至少派多少辆车运土,才能完成任务?
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
本题满分10分.(为方便答题,可在答题卡上画出你认为必要的图形)
如图,过原点的直线 和
和 与反比例函数
与反比例函数 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.

(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由;
(3)设P( ,
, ),Q(
),Q( ,
, )(x2 > x1 > 0)是函数
)(x2 > x1 > 0)是函数 图象上的任意两点,
图象上的任意两点, ,
, ,试判断
,试判断 ,
, 的大小关系,并说明理由.
的大小关系,并说明理由.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=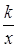 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).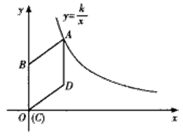
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=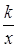 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(本小题满分10分)如图,A(-4,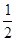 ),B(-1,2)是一次函数
),B(-1,2)是一次函数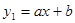 与反比例函数
与反比例函数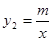 图象的两个交点, AC⊥
图象的两个交点, AC⊥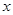 轴于点C,BD⊥
轴于点C,BD⊥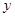 轴于点D。
轴于点D。
(1)根据图象直接回答:在第二象限内,当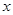 取何值时,
取何值时,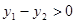 ?
?
(2)求一次函数解析式及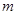 的值;
的值;
(3)P是线段AB上一点,连结PC,PD,若△PCA和△PDB面积相等,求点P的坐标。
如图,抛物线y=ax2+bx(a>0)与双曲线y= 相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.
相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积.若存在,请你写出点D的坐标;若不存在,请你说明理由.
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
试题篮
()