如图,反比例函数y= (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
如图,已知动点A在函数y=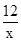 (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴、y轴于点P,Q.当QE∶DP=4∶9时,图中阴影部分的面积等于 .
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴、y轴于点P,Q.当QE∶DP=4∶9时,图中阴影部分的面积等于 .
如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
如图,点P在双曲线 (x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .
(x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .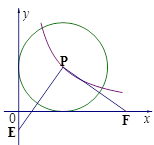
反比例函数y1= ,y2=
,y2= (k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .
(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .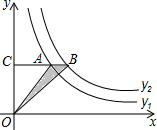
如图,在平面直角坐标系中直线 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线 向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是 .
的图象经过点C,交AB于点D,则点D的坐标是 .
如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数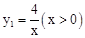 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是 .
的图象经过点C,交AB于点D,则点D的坐标是 .
如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数 (填函数解析式)的图象上运动.
如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点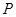 落在反比例函数
落在反比例函数 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在 轴上,一个顶点落在
轴上,一个顶点落在 轴上.
轴上.
(1)图1中的每一个小正方形的面积是 ;
(2)按照图1 图2
图2 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第 个图形中每一个小正方形的面积是 .(用含
个图形中每一个小正方形的面积是 .(用含 的代数式表示)
的代数式表示)
如图,点P是反比例函数
图象上的点,PA垂直x轴于点A
,点
的坐标为
,
交y轴于点
,连结
,已知
。

(1)k的值是
;
(2)若
是该反比例函数图象上的点,且满足
,则a的取值范围是。
两个反比例函数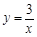 ,
, 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点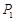 ,
, ,
,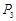 ,…,
,…,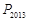 在函数
在函数 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是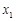 ,
, ,
, ,…,
,…,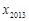 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点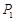 ,
, ,
,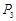 ,…,
,…,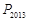 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数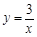 的图像交点依次是
的图像交点依次是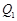 (
(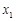 ,
,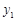 ),
),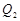 (
( ,
,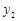 ),
),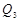 (
( ,
,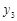 ),…,
),…, (
(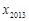 ,
,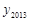 ),则
),则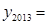 .
.
如图,A、B分别是反比例函数 图象上的点,过A、B作
图象上的点,过A、B作 轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为
轴的垂线,垂足分别为C、D,连接OB、OA,OA交BD于E点,△BOE的面积为 ,四边形ACDE的面积为
,四边形ACDE的面积为 ,则
,则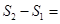 .
.
如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ 上,B、D在双曲线y2=
上,B、D在双曲线y2= 上,k1=2k2(k1>0),AB∥y轴,S▱ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S▱ABCD=24,则k1= .
试题篮
()