初中数学平行线分线段成比例试题

国际比赛的足球场地是在100米到110米之间，宽是在64米到75米之间，现有一个长方形的足球场，其长是宽的1.5倍，面积是7560平方米，那么这个足球场能用作国际比赛吗？（参考数据：）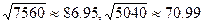

已知：如图，在平面直角坐标系xOy中，直线与轴交于点A (– 2，0)，与反比例函数在第一象限内的图象交于点B (2，n)，连结BO，若．

（1）求该反比例函数的解析式和直线的解析式；
（2）若直线AB与轴的交点为C，求△OCB的面积．

已知点A，B和点C在反比例函数上，若，则的大小关系是（    ）

A．	B．
C．	D．

如图，反比例函数的图象过矩形OABC的顶点B，OA、OC分别在x轴、
y轴的正半轴上，OA：OC=2：1．
（1）设矩形OABC的对角线交于点E，求出E点的坐标；
（2）若直线平分矩形OABC面积，求的值．

如图，P₁是反比例函数在第一象限图像上的一点，点A₁的坐标为(2，0)．
（1）当点P₁的横坐标逐渐增大时，△P₁O A₁的面积
将如何变化？
（2）若△P₁O A₁与△P₂ A₁ A₂均为等边三角形，求
此反比例函数的解析式及A₂点的坐标．

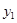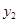已知点（-1，），（2，），（3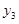，）在反比例函数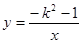的图像上. 下列结论中正确的是

A．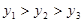

B．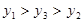

C．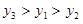

D．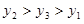

（1）（本小题满分4分）—+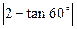
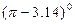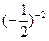
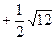
（2）（本小题满分6分）已知：y＝y₁＋y₂，y₁与x²成正比例，y₂与x成反比例，且
x＝1时，y＝3；x＝-1时，y＝1. 求x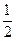＝-时，y的值．

若反比例函数的图象经过点（－3，2），则的值为 （    ）．

A．－6

B．6

C．-5

D．5