如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()
AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()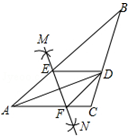
A.2 B.4 C.6 D.8
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作射线PE⊥PD,与线段AB交于点E,则线段PC的范围是()
| A.PC>0 | B.0<PC<12 | C.3≤PC≤12 | D.3<PC<12 |
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为()
A、 B、
B、 C、
C、 D、
D、
如图,Rt△ABC中,∠ACB=Rt∠,AC=2BC=2,作内接正方形A1B1D1C;在Rt△AA1B1中,作内接正方形A2B2D2A1;在Rt△AA2B2中,作内接正方形A3B3D3A2;……;依次作下去,则第n个正方形AnBnDnAn-1的边长是()
A. |
B. |
C. |
D. |
如图,□ABCD的面积为20,点E,F,G为对角线AC的四等分点,连接BE并延长交AD于H,连接HF并延长交BC于点M,则△BHM的面积为()
| A.10 | B. |
C.4 | D.5 |
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为()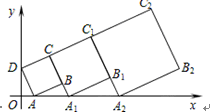
A.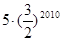 |
B.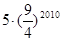 |
C.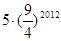 |
D.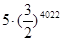 |
如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为使△DEM ∽△ABC,则点M所在位置应是F、G、H、K四点中的()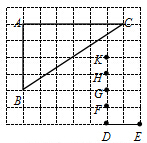
A.K B.H C.G D.F
如图,O是△ABC的外接圆的圆心,∠ABC=60°,BF,CE分别是AC,AB边上的高且交于点H,CE交⊙O于M,D,G分别在边BC,AB上,且BD=BH,BG=BO,下列结论:①∠ABO=∠HBC;②AB•BC=2BF•BH;③BM=BD;④△GBD为等边三角形,其中正确结论的序号是()
| A.①② | B.①③④ | C.①②④ | D.①②③④ |
如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C′处;作∠BPC′的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A. |
B. |
C. |
D. |
如图,点P是以O为圆心, AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C、D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是()
A.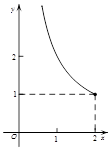 B.
B.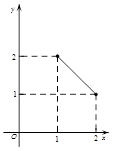 C.
C.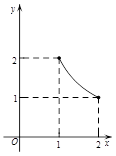 D.
D.
如图1,菱形ABCD的对角线交于点O,AC=2BD,点P是AO上一个动点,过点P作AC的垂线交菱形的边于M,N两点.设AP=x,△OMN的面积为y, 表示y与x的函数关系的图象大致如图2所示,则菱形的周长为()
| A.2 | B. |
C.4 | D.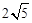 |
如图,在矩形 中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为()
A.( ,
, )、(
)、( ,
, )B.(
)B.( ,
, )、(
)、( ,
, )
)
C.( ,
, )、(
)、( ,
, )D.(
)D.( ,
, ) 、(
) 、( ,
, )
)
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
A. |
B. |
C.y=x | D. |
试题篮
()