初中数学相似多边形的性质选择题

下列生活现象中，属于相似变换的是（    ）

A．荡秋千	B．汽车挂雨器的运动
C．抽屉的拉升	D．投影片的文字经投影变换到屏幕

如图，王华晚上由路灯A下的B处走到Ｃ处时，测得影子CD的长为１米，继续往前走３米到达Ｅ处时，测得影子EF的长为2米，已知王华的身高是1.5米，那么路灯A的高度AB等于（    ）

A．4.5米

B．6米

C．7.2米

D．8米

如图，为测量被荷花池相隔的两树A，B的距离，数学活动小组设计了如图所示的测量方案：在AB的垂线AP上取两点C，E，再定出AP的垂线FE，使F，C，B在一条直线上．其中三位同学分别测量出了三组数据：①AC，BC　　　②AC，CE　　③EF，CE，AC．能根据所测数据，求得A，B两树距离的是（　　）
A．②     B．①②       C．②③        D．①③

如图，在△ABC中，点D、E分别是AB、AC的中点，则下列结论不正确的是【   】

　　A．BC=2DE　　B．△ADE∽△ABC　　C．   　D．S_△ABC=3S_△ADE

某一时刻，身高1.6m 的小明在阳光下的影长是0.4m．同一时刻同一地点，测得某旗杆的影长是5m，则该旗杆的高度是

A．l.25m

B．10m

C．20m

D．8m

如图，身高为1.5米的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3米 , CA=1米, 则树的高度为（   ）

A． 4.5米

B． 6米

C．3米

D． 4米

                          

下列四个三角形，与左图中的三角形相似的是

如图，在正五边形ABCDE中，对角线AD、AC与EB分别相交于点M、N．下列命题：①四边形EDCN是菱形；②四边形MNCD是等腰梯形；③△AEN与△EDM全等；④△AEM与△CBN相似；⑤点M是线段AD、BE、NE的黄金分割点，其中假命题有（    ）
A．0个        B．1个       C．2个         D．4个

（第8题图）             

如图，在□ABCD中，点E为AD的中点，连接BE交AC于点F，则AF：CF=（    ）

A．1：2

B．1：3

C．2：3

D．2：5

如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG＝GC；③AG∥CF；④S_△FGC＝3．其中正确结论的个数是(  )

A．1

B．2

C．3

D．4

如图，从图甲到图乙的变换是（     ）

A．轴对称变换

B．平移变换

C．旋转变换

D．相似变换

 
甲           乙

在△ABC与△A′B′C′中，有下列条件：（1）；（2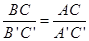）；（3）∠A=∠A′；（4）∠C=∠C′．如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有多少组（  ）

A．1

B．2

C．3

D．4

在Rt△ABC中，ÐC=90°，若将各边长度都扩大为原来的2倍，则ÐA的正弦值（  ）

A．扩大2倍

B．缩小2倍

C．扩大4倍

D．不变

若两个相似多边形的面积之比为1∶3，则对应边的比为（   ）

A．1∶3

B．3∶1

C．

D．

如图，是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB="1.2" m，BP="1.8" m，PD="12" m， 那么该古城墙的高度是：

A．6 m

B．8 m

C．18 m

D．24 m