如图,已知在△ABC,P为AB上一点,连结CP,不能判断△ABC~△ACP的是( )
| A.∠ACP=∠B | B.∠APC=∠ACB |
C. = = |
D. = = |
已知线段a=2,b=4,则线段a,b的比例中项为( )
| A.3 | B.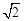 |
C.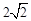 |
D.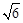 |
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD相交于点F,DE∶EC=2∶3,则 等于( )
等于( )
| A.4∶25 | B.4∶9 | C.9∶25 | D.2∶3 |
我们已经学习了相似三角形,也知道,如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.比如两个正方形,它们的边长、对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形,是相似图形的有( )
| A.①③ | B.①② | C.①④ | D.②③ |
在△ 和△
和△ 中,下列命题中真命题的个数为( ).
中,下列命题中真命题的个数为( ).
(1)若 ,
, ,则△
,则△ ∽△
∽△ ;
;
(2)若 ,
, ,则△
,则△ ∽△
∽△ ;
;
(3)若 ,
, (
( ),
), ,则△
,则△ ∽△
∽△ ;
;
(4)若 ,则△
,则△ ∽△
∽△ .
.
| A.1 | B.2 | C.3 | D.4 |
如图,△ABC中, 、
、 分别是
分别是 、
、 的中点,给出下列结论:
的中点,给出下列结论: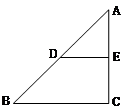
① ;②
;②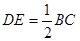 ;③
;③ ;④
;④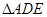 ∽
∽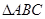 .
.
其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于( )
| A.40° | B.60° | C.80° | D.100° |
线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,将线段AB缩小为原来的 后得到对应的线段CD,则端点C的坐标为
后得到对应的线段CD,则端点C的坐标为
| A.(3,3) | B.(3,3)或 (-3,-3) | C.(-4,-1) | D.(4,1) |
若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
| A.1:4 | B.1:2 | C.2:1 | D.4:1 |
试题篮
()